

| A. | 91 | B. | 127 | C. | 169 | D. | 255 |
分析 由图形可知:第一层有1个花盆,第二层有1+6=7个花盆,第三层有1+6+12=19个花盆,第四层有1+6+12+18=37个花盆,…第n层有1+6×(1+2+3+4+…+n-1)=1+3n(n-1)个花盆,这垛花盆底层最长的一排共有13个花盆,也就是第7层,由此代入求得答案即可.
解答 解:∵第一层有1个花盆,
第二层有1+6=7个花盆,
第三层有1+6+12=19个花盆,
第四层有1+6+12+18=37个花盆,
…
∴第n层有1+6×(1+2+3+4+…+n-1)=1+3n(n-1)个花盆,
∵这垛花盆底层最长的一排共有13个花盆,
∴处于第7层,
∴花盆的个数是1+3×7×(7-1)=127.
故选:B.
点评 此题考查图形的变化规律,找出数字之间的运算规律,利用规律解决问题.


科目:初中数学 来源: 题型:解答题
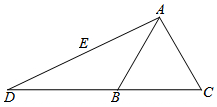 如图,延长等边三角形ABC一边CB到D,连接AD.以A为圆心,AC为半径画弧交AD于E.已知AC=2,∠D=20°,求DE的长(精确到0.1).(参考数据:$\sqrt{3}$≈1.73,tan20°≈0.36,sin20°≈0.34,cos20°≈0.94)
如图,延长等边三角形ABC一边CB到D,连接AD.以A为圆心,AC为半径画弧交AD于E.已知AC=2,∠D=20°,求DE的长(精确到0.1).(参考数据:$\sqrt{3}$≈1.73,tan20°≈0.36,sin20°≈0.34,cos20°≈0.94)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (3-x)(3+x)=9-x2 | B. | (a-b)(a2+ab+b2)=a3-b3 | ||
| C. | a2-4ab+4b2-1=a(a-4b)+(2b+1)(2b-1) | D. | 4x2-25y2=(2x+5y)(2x-5y) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年四川达县万家中学下学期九年级第一次月考数学试卷(解析版) 题型:解答题
某公司为了更好得节约能源,决定购买一批节省能源的10台新机器。现有甲、乙两种型号的设备,其中每台的价格、工作量如下表。经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台甲型设备比购买3台乙型设备少6万元.
甲型 | 乙型 | |
价格(万元/台) |
|
|
产量(吨/月) | 240 | 180 |
(1)求a, b的值;
(2)经预算:该公司购买的节能设备的资金不超过110万元,请列式解答有几种购买方案可供选择;
(3)在(2)的条件下,若每月要求产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com