

���� ��1����A��B������������ô���ϵ���������ֱ��AB�Ľ���ʽ��
��2���ֱ��A��B������AB�Ĵ��ߣ���������Ľ��㼴Ϊ�����M�㣬�ٽ�����������ε��������OM�ij�������õ�M�����ꣻ
��3����A�ֱ���x���y��Ĵ��ߣ�����ֱ�ΪE��F����֤����AEC�ա�AFD���ɵõ�EC=FD���Ӷ��ɰ�OC-ODת��ΪFD-OD���������߶εĺͲ�����OC-OD=OE+OF=8��
��� �⣺
��1����ֱ��AB�Ľ���ʽΪ��y=kx+b��k��0����
�ߵ�A��-4��4������B��0��2����ֱ��AB�ϣ�
��$\left\{\begin{array}{l}{-4k+b=4}\\{b=2}\end{array}\right.$�����$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=2}\end{array}\right.$��
��ֱ��AB�Ľ���ʽΪ��y=-$\frac{1}{2}$x+2��
��2���ߡ�ABM����ABΪֱ�DZߵ�ֱ�������Σ�
���С�BAM=90����ABM=90�㣬
�ٵ���BAM=90��ʱ����ͼ1��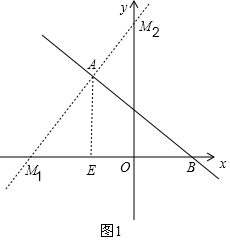
��A��AB�Ĵ��ߣ���x���ڵ�M1����y���ڵ�M2��
���֪��AEM1�ס�BEA��
��$\frac{{M}_{1}E}{AE}$=$\frac{AE}{BE}$��
�ɣ�1����֪OE=OB=AE=4��
��$\frac{{M}_{1}E}{4}$=$\frac{4}{8}$�����M1E=2��
��OM1=2+4=6��
��M1��-6��0����
��AE��y�ᣬ
��$\frac{{M}_{1}E}{{M}_{1}O}$=$\frac{AE}{O{M}_{2}}$����$\frac{2}{6}$=$\frac{4}{O{M}_{2}}$�����OM2=12��
��M2��0��12����
�ڵ���ABM=90��ʱ����ͼ2��
��B��AB�Ĵ��ߣ���y���ڵ�M3��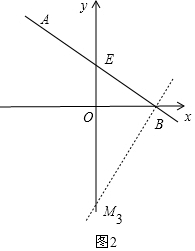
��ֱ��AB��y���ڵ�E�����ɣ�1����֪E��0��2����
��OE=2��OB=4��
�������֪��BOE�ס�M3OB��
��$\frac{OE}{OB}$=$\frac{OB}{O{M}_{3}}$����$\frac{2}{4}$=$\frac{4}{O{M}_{3}}$�����OM3=8��
��M3��0��-8����
���Ͽ�֪��M������Ϊ��-6��0����0��12����0��-8����
��3�����䣮
�������£�
����A�ֱ���x�ᡢy��Ĵ��ߣ�����ֱ�ΪG��H����ͼ3��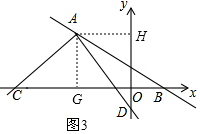
���AGC=��AHD=90�㣬
�֡ߡ�HOC=90�㣬
���GAH=90�㣬
���DAG+��DAH=90�㣬
�ߡ�CAD=90�㣬
���DAG+��CAG=90�㣬
���CAG=��DAH��
��A��-4��4����
��OG=AH=AG=OH=4��
�ڡ�AGC�͡�AHD��
$\left\{\begin{array}{l}{��AGC=��AHD}\\{AG=AH}\\{��CAG=��DAH}\end{array}\right.$
���AGC�ա�AHD��ASA����
��GC=HD��
��OC-OD=��OG+GC��-��HD-OH��=OG+OH=8��
��OC-OD��ֵ�������仯��ֵΪ8��
���� ����Ϊһ�κ������ۺ�Ӧ�ã��漰֪ʶ���д���ϵ������ȫ�������ε��ж������ʡ����������ε��ж������ʼ���������˼��ȣ��ڣ�1����ע�����ϵ������Ӧ�ò��裬�ڣ�2����ȷ����M���λ���ǽ���Ĺؼ����ڣ�3���й���������ȫ���ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���Ѷ����У�


 �ظ���ʦ�㲦ϵ�д�
�ظ���ʦ�㲦ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | $\sqrt{3}$ | C�� | ��3 | D�� | $��\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���Ի���С�� | B�� | �������� | ||
| C�� | ��2��ƽ���� | D�� | ����ֵ��0��1֮�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 6 | B�� | 10 | C�� | 3 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 �ڵȱ�������ABC�У�D��E�ֱ���BC��AC���е㣬��P���߶�AD�ϵ�һ�����㣬����PCE���ܳ���Сʱ��P���λ���ڣ�������
�ڵȱ�������ABC�У�D��E�ֱ���BC��AC���е㣬��P���߶�AD�ϵ�һ�����㣬����PCE���ܳ���Сʱ��P���λ���ڣ�������| A�� | ��ABC�����Ĵ� | B�� | AD���е㴦 | C�� | A�㴦 | D�� | D�㴦 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com