
【题目】如图,在□ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF

(1)求证:四边形ABEF是菱形;
(2)若AE=6,BF=8,CE=![]() ,求□ABCD的面积.
,求□ABCD的面积.
【答案】(1)证明见解析(2)36
【解析】试题分析:(1)根据平行四边形的性质和角平分线的性质得到四边形ABEF是平行四边形,然后再根据一组领边相等的平行四边形是菱形,证得结论;
(2)过点A作AH⊥BC于点H.根据菱形的对角线求出边长,然后根据面积的不变性求出平行四边形的高,从而求解.
试题解析:(1)证明:∵在□ABCD中,
∴AD∥BC.∴∠DAE=∠AEB.
∵∠BAD的平分线交BC于点E,
∴∠DAE=∠BAE.
∴∠BAE=∠AEB.
∴AB=BE.
同理AB=AF.
∴AF=BE.
∴四边形ABEF是平行四边形.
∵AB=BE.
∴四边形ABEF是菱形.
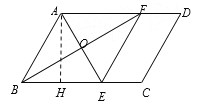
(2)解法一:过点A作AH⊥BC于点H.
∵四边形ABEF是菱形,AE=6,BF=8,
∴AE⊥BF,OE=3,OB=4.∴BE=5.
∵S菱形ABEF=![]() AEBF=BEAH,∴AH=
AEBF=BEAH,∴AH=![]() ×6×8÷5=
×6×8÷5=![]() .
.
∴S□ABCD=BCAH=(5+![]() )×
)×![]() =36.
=36.
解法二:∵四边形ABEF是菱形,AE=6,BF=8,
∴AE⊥BF,OE=3,OB=4.∴BE=5.
∵S菱形ABEF=![]() AEBF=
AEBF=![]() ×6×8=24,
×6×8=24,
∵CE=![]() ,BE=5,
,BE=5,
∴S□ABCD=![]() S菱形ABEF =
S菱形ABEF =![]() ×24=36.
×24=36.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
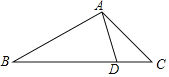
【题目】如图,D是△ABC的边BC上一点,AB=4,AD=2,∠DAC=∠B.如果△ABD的面积为15,那么△ACD的面积为( )
A. 15 B. 10 C. ![]() D. 5
D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
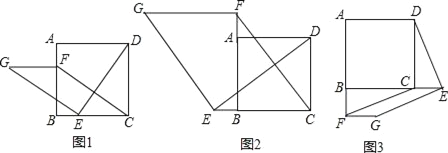
【题目】如图1,在正方形ABCD中,点E、F分别是边BC、AB上的点,且CE=BF,连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.
(1)请判断:FG与CE的数量关系和位置关系;(不要求证明)
(2)如图2,若点E、F分别是CB、BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请给出判断并予以证明;
(3)如图3,若点E、F分别是BC、AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,二次函数![]() ≠0
≠0![]() 的图像经过点(3,5)、(2,8)、(0,8).
的图像经过点(3,5)、(2,8)、(0,8).
①求这个二次函数的解析式;
②已知抛物线![]() ≠0
≠0![]() ,
,![]() ≠0
≠0![]() ,且满足
,且满足![]() ≠0,1
≠0,1![]() ,则我们称抛物线
,则我们称抛物线![]() 互为“友好抛物线”,请写出当
互为“友好抛物线”,请写出当![]() 时第①小题中的抛物线的友好抛物线,并求出这“友好抛物线”的顶点坐标.
时第①小题中的抛物线的友好抛物线,并求出这“友好抛物线”的顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列条件中:①∠A +∠B=∠C;②∠A:∠B:∠C=l:2:3;③∠A=90°-∠B;④∠A=∠B=![]() ∠C中,能确定△ABC是直角三角形的条件有( )
∠C中,能确定△ABC是直角三角形的条件有( )
A. 1个; B. 2个; C. 3个; D. 4个;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为实施国家“营养早餐”工程,食堂用甲、乙两种原料配制成某种营养食品,已知这两种原料的维生素c含量及购买这两种原料的价格如下表:

现要配制这种营养食品20 千克,要求每千克至少含有480 单位的维生素c,设购买甲种原料x千克.
(1)至少需要购买甲种原料多少千克?
(2)设食堂用于购买这两种原料的总费用为y 元,求 y与x的函数关系式,并说明购买甲种原料多少千克时,总费用最少。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1) 一10+8÷(一2)3一(一40)×(一3);
(2) 一2+|5一8|+24÷(一3);
(3) [30一(![]() 十
十![]() 一
一![]() )×36]÷(一5);
)×36]÷(一5);
(4) [53—4×(一5)2一(一1)10]÷(一24—24+24).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com