【题目】计算：
(1) 一10+8÷（一2）3一（一40）×（一3）；
(2) 一2+|5一8|+24÷(一3);
(3) [30一（
十
一
）×36]÷(一5)；
(4) [53—4×（一5）2一（一1）10]÷（一24—24+24）．
【答案】 (1)－131； (2)－7；(3)－1；(4)－1．
【解析】试题分析：（1）原式先计算乘方运算，再计算乘除运算，最后算加减运算即可得到结果；
（2）原式先计算除法运算，再计算加减运算即可得到结果；
（3）原式先计算乘除运算，再计算加减运算即可得到结果；
（4）原式先计算乘方运算，再计算乘除运算，最后算加减运算即可得到结果．
试题解析：
(1)原式＝ －10+8÷（－8）－120＝－10+（－1）－120＝－131；
(2)原式＝－2+3－8＝－7；
(3)原式＝(30－28－30+33)÷（－5）＝5÷ (－5)＝－1；
(4)原式＝ (125－4×25—1)÷（-24）＝24÷（一24）＝－1．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：①4ac＜b2；②方程ax2+bx+c=0的两个根是x1=﹣1，x2=3；③3a+c＜0④当y＞0时，x的取值范围是﹣1≤x＜3⑤当x＜0时，y随x增大而增大其中结论正确的个数是（ ）
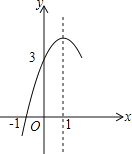
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在□ABCD中，∠BAD的平分线交BC于点E，∠ABC的平分线交AD于点F，AE与BF相交于点O，连接EF
（1）求证：四边形ABEF是菱形；
（2）若AE＝6，BF＝8，CE＝
，求□ABCD的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知直线y=x+3与 x轴、y轴交于A,B两点，直线
经过原点，与线段AB交于点C，使△AOC的面积与△BOC的面积之比为2：1.
（1）求A、B两点的坐标；
（2）求直线的函数解析式；
（3）在坐标平面是否存在点M，使得以A、C、O、M为顶点的四边形是平行四边形，若没有请说明理由，若有请直接写出M点的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在一个箱子里放有1个白球和2个红球，它们除颜色外其余都相同．
（1）判断下列甲乙两人的说法，认为对的在后面括号内答“√”，错的打“×”．
甲：“从箱子里摸出一个球是白球或者红球”这一事件是必然事件 ；
乙：从箱子里摸出一个球，记下颜色后放回，搅匀，这样连续操作三次，其中必有一次摸到的是白球 ；
（2）小明说：从箱子里摸出一个球，不放回，再摸出一个球，则“摸出的球中有白球”这一事件的概率为
，你认同吗？请画树状图或列表计算说明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列关于x的方程，一定是一元二次方程的是（ ）
A. x2﹣2xy=0 B. （x+1）（x﹣1）=x2﹣2x
C. ax2+bx+c=0 D. （m2+1）x2﹣2x﹣3=0
查看答案和解析>>
科目：初中数学 来源： 题型：
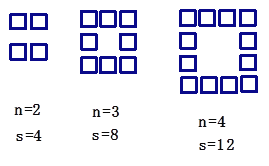
【题目】观察右面的图案，每条边上有n（n≥2）个方点，每个图案中方点的总数是S.
（1）请写出n=5时， S= ；
（2）请写出n=18时，S= ；
（3）按上述规律，写出S与n的关系式 S= ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】先阅读下列解题过程，然后回答问题：
解方程： 
解：①当
≥0时，原方程可化为： 
，解得
；
②当
＜0时，原方程可化为： 
，解得
；
所以原方程的解是
或
（1）解方程： 
（2）探究：当
为何值时，方程
①无解；②只有一个解；③有两个解。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com