
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①4ac<b2;②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;③3a+c<0④当y>0时,x的取值范围是﹣1≤x<3⑤当x<0时,y随x增大而增大其中结论正确的个数是( )
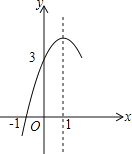
A. 5个 B. 4个 C. 3个 D. 2个
【答案】C
【解析】利用抛物线与x轴的交点个数可对①进行判断;利用抛物线的对称性得到抛物线与x轴的一个交点坐标为(3,0),则可对②进行判断;由对称轴方程得到b=﹣2a,然后根据x=﹣1时函数值为负数可得到3a+c<0,则可对③进行判断;根据抛物线在x轴上方所对应的自变量的范围可对④进行判断;根据二次函数的性质对⑤进行判断.
解:∵抛物线与x轴有2个交点,∴b2﹣4ac>0,所以①正确;
∵抛物线的对称轴为直线x=1,而点(﹣1,0)关于直线x=1的对称点的坐标为(3,0),∴方程ax2+bx+c=0的两个根是x1=﹣1,x2=3,所以②正确;
∵x=﹣![]() =1,即b=﹣2a,而x=﹣1时,y<0,即a﹣b+c<0,∴a+2a+c<0,所以③错误;
=1,即b=﹣2a,而x=﹣1时,y<0,即a﹣b+c<0,∴a+2a+c<0,所以③错误;
∵抛物线与x轴的两点坐标为(﹣1,0),(3,0),∴当﹣1<x<3时,y>0,所以④错误;
∵抛物线的对称轴为直线x=1,∴当x<1时,y随x增大而增大,所以⑤正确.
故选C.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】把“直角三角形,等腰三角形,等腰直角三角形”填入下列相应的空格上.
(1)正方形可以由两个能够完全重合的 _________ 拼合而成;
(2)菱形可以由两个能够完全重合的 _________ 拼合而成;
(3)矩形可以由两个能够完全重合的 _________ 拼合而成.
查看答案和解析>>
科目:初中数学 来源: 题型:
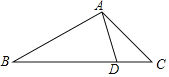
【题目】如图,D是△ABC的边BC上一点,AB=4,AD=2,∠DAC=∠B.如果△ABD的面积为15,那么△ACD的面积为( )
A. 15 B. 10 C. ![]() D. 5
D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
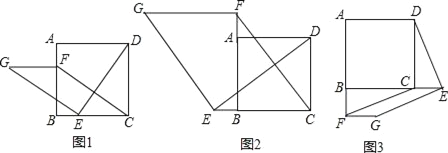
【题目】如图1,在正方形ABCD中,点E、F分别是边BC、AB上的点,且CE=BF,连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.
(1)请判断:FG与CE的数量关系和位置关系;(不要求证明)
(2)如图2,若点E、F分别是CB、BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请给出判断并予以证明;
(3)如图3,若点E、F分别是BC、AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,二次函数![]() ≠0
≠0![]() 的图像经过点(3,5)、(2,8)、(0,8).
的图像经过点(3,5)、(2,8)、(0,8).
①求这个二次函数的解析式;
②已知抛物线![]() ≠0
≠0![]() ,
,![]() ≠0
≠0![]() ,且满足
,且满足![]() ≠0,1
≠0,1![]() ,则我们称抛物线
,则我们称抛物线![]() 互为“友好抛物线”,请写出当
互为“友好抛物线”,请写出当![]() 时第①小题中的抛物线的友好抛物线,并求出这“友好抛物线”的顶点坐标.
时第①小题中的抛物线的友好抛物线,并求出这“友好抛物线”的顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1) 一10+8÷(一2)3一(一40)×(一3);
(2) 一2+|5一8|+24÷(一3);
(3) [30一(![]() 十
十![]() 一
一![]() )×36]÷(一5);
)×36]÷(一5);
(4) [53—4×(一5)2一(一1)10]÷(一24—24+24).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com