
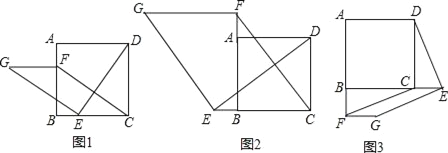
【题目】如图1,在正方形ABCD中,点E、F分别是边BC、AB上的点,且CE=BF,连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.
(1)请判断:FG与CE的数量关系和位置关系;(不要求证明)
(2)如图2,若点E、F分别是CB、BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请给出判断并予以证明;
(3)如图3,若点E、F分别是BC、AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.
【答案】(1)FG = CE, FG ∥ CE;
(2)仍然成立,证明见解析;
(3)FG = CE , FG ∥ CE仍然成立. 。
【解析】试题分析:(1)结论:FG=CE,FG∥CE.如图1中,设DE与CF交于点M,首先证明△CBF≌△DCE,推出DE⊥CF,再证明四边形EGFC是平行四边形即可.(2)结论仍然成立.如图2中,设DE与CF交于点M,首先证明△CBF≌△DCE,推出DE⊥CF,再证明四边形EGFC是平行四边形即可.(3)结论仍然成立.如图3中,设DE与FC的延长线交于点M,证明方法类似.
试题解析:(1)结论:FG=CE,FG∥CE.

理由:图1中,设DE与CF交于点M.
∵四边形ABCD是正方形,
∴BC=CD,∠ABC=∠DCE=90°,
在△CBF和△DCE中,
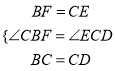 ,
,
∴△CBF≌△DCE,
∴∠BCF=∠CDE,CF=DE,
∵∠BCF+∠DCM=90°,
∴∠CDE+∠DCM=90°,
∴∠CMD=90°,
∴CF⊥DE,
∵GE⊥DE,
∴EG∥CF,
∵EG=DE,CF=DE,
∴EG=CF,
∴四边形EGFC是平行四边形。
∴GF=EC,
∴GF=EC,GF∥EC.
(2)结论仍然成立。
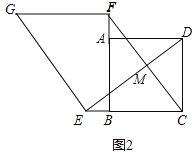
理由:如图2中,设DE与CF交于点M.
∵四边形ABCD是正方形,
∴BC=CD,∠ABC=∠DCE=90,
在△CBF和△DCE中,
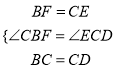 ,
,
∴△CBF≌△DCE,
∴∠BCF=∠CDE,CF=DE,
∵∠BCF+∠DCM=90°,
∴∠CDE+∠DCM=90°,
∴∠CMD=90°,
∴CF⊥DE,
∵GE⊥DE,
∴EG∥CF,
∵EG=DE,CF=DE,
∴EG=CF,
∴四边形EGFC是平行四边形。
∴GF=EC,
∴GF=EC,GF∥EC.
(3)结论仍然成立。

理由:如图3中,设DE与FC的延长线交于点M.
∵四边形ABCD是正方形,
∴BC=CD,∠ABC=∠DCE=90,
∴∠CBF=∠DCE=90
在△CBF和△DCE中,
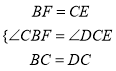 ,
,
∴△CBF≌△DCE,
∴∠BCF=∠CDE,CF=DE
∵∠BCF+∠DCM=90°,
∴∠CDE+∠DCM=90°,
∴∠CMD=90°,
∴CF⊥DE,
∵GE⊥DE,
∴EG∥CF,
∵EG=DE,CF=DE,
∴EG=CF,
∴四边形EGFC是平行四边形。
∴GF=EC,
∴GF=EC,GF∥EC.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】抛物线y=-2x2经过平移后得到抛物线y=-2x2-4x-5,平移方法是( )
A. 向左平移1个单位,再向下平移3个单位
B. 向左平移1个单位,再向上平移3个单位
C. 向右平移1个单位,再向下平移3个单位
D. 向右平移1个单位,再向上平移3个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上):
①把△ABC沿BA方向平移,请在网格中画出当点A移动到点A1时的△A1B1C1;
②把△A1B1C1绕点A1按逆时针方向旋转90°后得到△A2B2C2,如果网格中小正方形的边长为1,求点B1旋转到B2的路径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①4ac<b2;②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;③3a+c<0④当y>0时,x的取值范围是﹣1≤x<3⑤当x<0时,y随x增大而增大其中结论正确的个数是( )
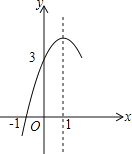
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列判断:
①若|m|>0,则m>0;
②若m>n,则|m|>|n|;
③若|m|>|n|,则m>n;
④任意数m,则|m|是正数;
⑤在数轴上,离原点越远,该点对应的数的绝对值越大,
其中正确的结论的个数为( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=2![]() ,AD=4,点E是BC边上一个动点,连接AE,作DF⊥AE于点F,当BE的长为_____________________时,△CDF是等腰三角形.
,AD=4,点E是BC边上一个动点,连接AE,作DF⊥AE于点F,当BE的长为_____________________时,△CDF是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF

(1)求证:四边形ABEF是菱形;
(2)若AE=6,BF=8,CE=![]() ,求□ABCD的面积.
,求□ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于x的方程,一定是一元二次方程的是( )
A. x2﹣2xy=0 B. (x+1)(x﹣1)=x2﹣2x
C. ax2+bx+c=0 D. (m2+1)x2﹣2x﹣3=0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com