Question

【题目】如图，已知直线y=x+3与 x轴、y轴交于A,B两点，直线经过原点，与线段AB交于点C，使△AOC的面积与△BOC的面积之比为2：1.

（1）求A、B两点的坐标；

（2）求直线的函数解析式；

（3）在坐标平面是否存在点M，使得以A、C、O、M为顶点的四边形是平行四边形，若没有请说明理由，若有请直接写出M点的坐标.

Answer 1

【答案】（1）A(-3,0)，B(0,3)；（2） （3）M1(-4,2)，M2(2,2)，M3(-2,-2)

【解析】（1）令y=0和x=0即可分别求出A、B两点坐标；

（2）根据△AOC的面积与△BOC的面积之比为2：1.可求出点C的坐标，再利用待定系数法即可求出直线的函数解析式；

（3）以AC、AO、CO三边分别为平行四边形的对角线即可得出点M的坐标.

解：（1）当y=0时，则x+3＝0

解得，x＝-3,

∴A(-3,0)

当x=0时，则y=0+3＝3

∴B(0,3)

（2）设直线为

∵A(-3,0) B(0,3)

∴S△AOB=

∵S△AOC:S△BOC=2:1

∴S△AOC=S△AOB=3

又∵AO=3

∴△AOC的AO边上的高为2，即C点的纵坐标为2

又∵C点在直线上

∴ C(-1,2)

又∵C点在直线上

∴直线为

（3）存在点M，使得以A、C、O、M为顶点的四边形是平行四边形.

如图所示：

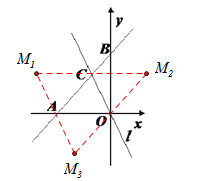
∴M1(-4,2),M2(2,2),M3(-2,-2)