
【题目】如图,![]() 中,
中,![]() ,
,![]() 是边
是边![]() 上的中线,分别过点
上的中线,分别过点![]() ,
,![]() 作
作![]() ,
,![]()
的平行线交于点![]() ,且
,且![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证:四边形![]() 是菱形;
是菱形;
(2)若![]() ,求
,求![]() 的值.
的值.

【答案】(1)证明过程见解析;(2)![]()
【解析】
试题分析:(1)、根据平行得出DBCE为平行四边形,根据CE=BD,CD是中线得出BD=AD,则CE=DA,结合CE∥DA得出ADCE为平行四边形,根据∠BCA=90°,CD为中线得出AD=CD,则四边形ADCE为菱形;(2)、作CF⊥AB,设BC=x,则AC=2x,根据Rt△ABC的勾股定理得出AB=![]() x,根据面积法得出CF的长度,然后进行计算sin∠CDB的值.
x,根据面积法得出CF的长度,然后进行计算sin∠CDB的值.
试题解析:(1)、∵![]() ,
,![]() ,∴四边形
,∴四边形![]() 是平行四边形.∴
是平行四边形.∴![]() .
.
又∵![]() 是边
是边![]() 上的中线,∴
上的中线,∴![]() . ∴
. ∴![]() .又∵
.又∵![]() ,∴四边形
,∴四边形![]() 是平行四边形.
是平行四边形.
∵![]() ,
,![]() 是斜边
是斜边![]() 上的中线,∴
上的中线,∴![]() .∴四边形
.∴四边形![]() 是菱形.
是菱形.
(2)、作![]() 于点
于点![]() .由(1) 可知,
.由(1) 可知, ![]() 设
设![]() ,则
,则![]() .
.
在![]() 中,根据勾股定理可求得
中,根据勾股定理可求得![]() .∵
.∵![]() ,
,
∴![]() ∵
∵![]() , ∴
, ∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=2![]() ,AD=4,点E是BC边上一个动点,连接AE,作DF⊥AE于点F,当BE的长为_____________________时,△CDF是等腰三角形.
,AD=4,点E是BC边上一个动点,连接AE,作DF⊥AE于点F,当BE的长为_____________________时,△CDF是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=x+3与 x轴、y轴交于A,B两点,直线![]() 经过原点,与线段AB交于点C,使△AOC的面积与△BOC的面积之比为2:1.
经过原点,与线段AB交于点C,使△AOC的面积与△BOC的面积之比为2:1.
(1)求A、B两点的坐标;
(2)求直线![]() 的函数解析式;
的函数解析式;
(3)在坐标平面是否存在点M,使得以A、C、O、M为顶点的四边形是平行四边形,若没有请说明理由,若有请直接写出M点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于x的方程,一定是一元二次方程的是( )
A. x2﹣2xy=0 B. (x+1)(x﹣1)=x2﹣2x
C. ax2+bx+c=0 D. (m2+1)x2﹣2x﹣3=0
查看答案和解析>>
科目:初中数学 来源: 题型:
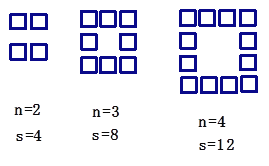
【题目】观察右面的图案,每条边上有n(n≥2)个方点,每个图案中方点的总数是S.
(1)请写出n=5时, S= ;
(2)请写出n=18时,S= ;
(3)按上述规律,写出S与n的关系式 S= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小乐用一块长方形硬纸板在阳光下做投影实验,通过观察,发现这块长方形硬纸板在平整的地面上不可能出现的投影是
A、三角形 B、线段 C、矩形 D、正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,∠D=100°,AC平分∠BCD,且∠ACB=40°,∠BAC=70°.
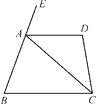
(1)AD与BC平行吗?试写出推理过程;
(2)求∠DAC和∠EAD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列对“0”的说法正确的个数是( )
①0是正数和负数的分界点;②0只表示“什么也没有”;③0可以表示特定的意义,如0℃;④0是正数;⑤0是自然数.
A. 3个 B. 4个 C. 5个 D. 0个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com