
【题目】已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
(1)求证:BD是⊙O的切线;
(2)求证:CE2=EHEA;
(3)若⊙O的半径为5,sinA= ![]() ,求BH的长.
,求BH的长.
【答案】
(1)证明:∵∠ODB=∠AEC,∠AEC=∠ABC,
∴∠ODB=∠ABC,
∵OF⊥BC,
∴∠BFD=90°,
∴∠ODB+∠DBF=90°,
∴∠ABC+∠DBF=90°,
即∠OBD=90°,
∴BD⊥OB,
∴BD是⊙O的切线.
(2)证明:连接AC,如图1所示:
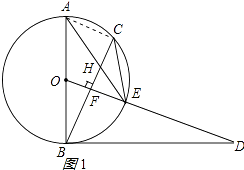
∵OF⊥BC,
∴ ![]() ,
,
∴∠CAE=∠ECB,
∵∠CEA=∠HEC,
∴△CEH∽△AEC,
∴ ![]() ,
,
∴CE2=EHEA;
(3)解:连接BE,如图2所示:
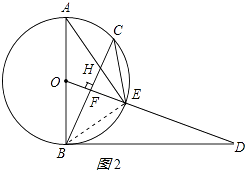
∵AB是⊙O的直径,
∴∠AEB=90°,
∵⊙O的半径为5,sin∠BAE= ![]() ,
,
∴AB=10,BE=ABsin∠BAE=10× ![]() =6,
=6,
∴EA= ![]() =
= ![]() =8,
=8,
∵ ![]() ,
,
∴BE=CE=6,
∵CE2=EHEA,
∴EH= ![]() =
= ![]() ,
,
在Rt△BEH中,BH= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)由圆周角定理和已知条件,证出∠ODB=∠ABC,再证出∠ABC+∠DBF=90°,即∠OBD=90°,即可得出BD是⊙O的切线;(2)连接AC,由垂径定理得出弧BE=弧CE,得出∠CAE=∠ECB,进而证明出△CEH∽△AEC,得出对应边成比例,即可得出结论;(3)连接BE,由圆周角定理得出∠AEB=90°,由三角函数求出BE的长,再根据勾股定理求出EA,得出BE=CE=6,由(2)的结论求出EH,最后根据勾股定理求出BH即可.


科目:初中数学 来源: 题型:
【题目】如图,已知BC=EC,∠BCE=∠ACD,如果只添加一个条件,使△ABC ≌ △DEC,则添加的条件不能为( )
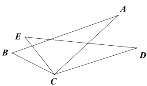
A. ∠B=∠E B. AC=DC C. ∠A=∠D D. AB=DE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若AB=3,BC=4,求四边形OCED的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a是最大的负整数,b、c满足(b-3)2+|c+4|=0,且a、b、c分别是点A、B、C在数轴上对应的数.
![]()
(1)点A表示的数为______,点B表示的数为______,点C表示的数为______;
(2)若动点P从C出发沿数轴正方向运动,点P的速度是每秒2个单位长度,运动几秒后,点P到点B为5个单位长度?
(3)在数轴上找一点M,使点M到A、B、C三点的距离之和等于13,请写出所有点M对应的数,并写出求解过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.
(1)已知BD= ![]() ,求正方形ABCD的边长;
,求正方形ABCD的边长;
(2)猜想线段EM与CN的数量关系并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鄂州某个体商户购进某种电子产品的进价是50元/个,根据市场调研发现售价是80元/个时,每周可卖出160个,若销售单价每个降低2元,则每周可多卖出20个.设销售价格每个降低x元(x为偶数),每周销售量为y个.
(1)直接写出销售量y个与降价x元之间的函数关系式;
(2)设商户每周获得的利润为W元,当销售单价定为多少元时,每周销售利润最大,最大利润是多少元?
(3)若商户计划下周利润不低于5200元的情况下,他至少要准备多少元进货成本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家之一.为了增强居民的节水意识,某市自来水公司对居民用水采用以户为单位分段计费办法收费.即一个月用水10 t以内(包括10 t)的用户,每吨收水费a元;一个月用水超过10 t的用户,10 t水仍按每吨a元收费,超过10 t的部分,按每吨b(b>a)元收费.设一户居民月用水x t,应交水费y元,y与x之间的函数关系如图所示.
(1)求a的值;某户居民上月用水8 t,应交水费多少元?
(2)求b的值,并写出当x>10时,y与x之间的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】是某汽车行驶的路程S(km)与时间t(min)的函数关系图.观察图中所提供的信息,解答下列问题:
(1)汽车在前9分钟内的平均速度是多少?
(2)汽车在中途停了多长时间?
(3)当16≤t≤30时,求S与t的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为统筹安排大课间体育活动,在各班随机选取了一部分学生,分成四类活动:“篮球”、“羽毛球”、“乒乓球”、“其他”进行调查,整理收集到的数据,绘制成如下的两幅统计图.
(1)学校采用的调查方式是;学校共选取了名学生;
(2)补全统计图中的数据:条形统计图中羽毛球人、乒乓球人、其他人、扇形统计图中其他 %;
(3)该校共有1200名学生,请估计喜欢“乒乓球”的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com