
【题目】如图1,AB是⊙O的直径,E是AB延长线上一点,EC切⊙O于点C,OP⊥AO交AC于点P,交EC的延长线于点D.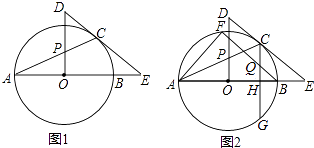
(1)求证:△PCD是等腰三角形;
(2)CG⊥AB于H点,交⊙O于G点,过B点作BF∥EC,交⊙O于点F,交CG于Q点,连接AF,如图2,若sinE= ![]() ,CQ=5,求AF的值.
,CQ=5,求AF的值.
【答案】
(1)解:连接OC,
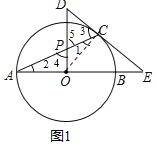
∵EC切⊙O于点C,
∴OC⊥DE,
∴∠1+∠3=90°,
又∵OP⊥OA,
∴∠2+∠4=90°,
∵OA=OC,
∴∠1=∠2,
∴∠3=∠4,
又∵∠4=∠5,
∴∠3=∠5,
∴DP=DC,即△PCD为等腰三角形
(2)解:如图2,连接OC、BC,
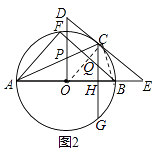
∵DE与⊙O相切于点E,
∴∠OCB+∠BCE=90°,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠OBC+∠BCE=90°,
又∵CG⊥AB,
∴∠OBC+∠BCG=90°,
∴∠BCE=∠BCG,
∵BF∥DE,
∴∠BCE=∠QBC,
∴∠BCG=∠QBC,
∴QC=QB=5,
∵BF∥DE,
∴∠ABF=∠E,
∵sinE= ![]() ,
,
∴sin∠ABF= ![]() ,
,
∴QH=3、BH=4,
设⊙O的半径为r,
∴在△OCH中,r2=82+(r﹣4)2,
解得:r=10,
又∵∠AFB=90°,sin∠ABF= ![]() ,
,
∴AF=12.
【解析】本题主要考查切线的性质、平行线的性质及三角函数的应用等知识的综合,根据切线性质和平行线性质及垂直性质证∠BCG=∠QBC是解题的关键.(1)连接OC,由切线性质和垂直性质得∠1+∠3=90°、∠2+∠4=90°,继而可得∠3=∠5得证;(2)连接OC、BC,先根据切线性质和平行线性质及垂直性质证∠BCG=∠QBC得QC=QB=5,而sinE=sin∠ABF= ![]() ,可知QH=3、BH=4,设圆的半径为r,在RT在△OCH中根据勾股定理可得r的值,在RT△ABF中根据三角函数可得答案.
,可知QH=3、BH=4,设圆的半径为r,在RT在△OCH中根据勾股定理可得r的值,在RT△ABF中根据三角函数可得答案.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°. 
(1)求BD的长;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60m到达C点,测得点B在点C的北偏东60°方向,如图2.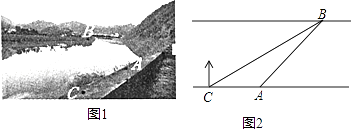
(1)求∠CBA的度数.
(2)求出这段河的宽(结果精确到1m,备用数据 ![]() ≈1.41,
≈1.41, ![]() ≈1.73).
≈1.73).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C:y=x2﹣2x+1的顶点为P,与y轴的交点为Q,点F(1, ![]() ).
).
(1)求点P,Q的坐标;
(2)将抛物线C向上平移得到抛物线C′,点Q平移后的对应点为Q′,且FQ′=OQ′.
①求抛物线C′的解析式;
②若点P关于直线Q′F的对称点为K,射线FK与抛物线C′相交于点A,求点A的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系内按下列要求完成作图(不要求写作法,保留作图痕迹).
(1)以(0,0)为圆心,3为半径画圆;
(2)以(0,﹣1)为圆心,1为半径向下画半圆;
(3)分别以(﹣1,1),(1,1)为圆心,0.5为半径画圆;
(4)分别以(﹣1,1),(1,1)为圆心,1为半径向上画半圆.
(向上、向下指在经过圆心的水平线的上方和下方)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(﹣2,0),B(2,0),C(3,5).
(1)求过点A,C的直线解析式和过点A,B,C的抛物线的解析式;
(2)求过点A,B及抛物线的顶点D的⊙P的圆心P的坐标;
(3)在抛物线上是否存在点Q,使AQ与⊙P相切,若存在请求出Q点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D、E,AD与BE相交于点F. 
(1)求证:△ACD∽△BFD;
(2)若∠ABD=45°,AC=3时,求BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com