
【题目】已知一次函数y1=ax+c和反比例函数y2= ![]() 的图象如图所示,则二次函数y3=ax2+bx+c的大致图象是( )
的图象如图所示,则二次函数y3=ax2+bx+c的大致图象是( ) 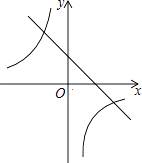
A.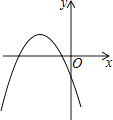
B.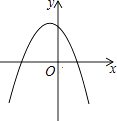
C.
D.
【答案】B
【解析】解:∵一次函数y1=ax+c图象过第一、二、四象限,
∴a<0,c>0,
∴二次函数y3=ax2+bx+c开口向下,与y轴交点在x轴上方;
∵反比例函数y2= ![]() 的图象在第二、四象限,
的图象在第二、四象限,
∴b<0,
∴﹣ ![]() <0,
<0,
∴二次函数y3=ax2+bx+c对称轴在y轴左侧.
满足上述条件的函数图象只有B选项.
故选B.
【考点精析】利用一次函数的图象和性质和反比例函数的图象对题目进行判断即可得到答案,需要熟知一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远;反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】某宾馆有50个房间供游客居住,当每个房间每天的定价为180元时,房间会全部住满;当每个房间每天的定价每增加10元时,就会有一个房间空闲.如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用.
(1)若每个房间定价增加40元,则这个宾馆这一天的利润为多少元?
(2)若宾馆某一天获利10640元,则房价定为多少元?
(3)房价定为多少时,宾馆的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AB是⊙O的直径,E是AB延长线上一点,EC切⊙O于点C,OP⊥AO交AC于点P,交EC的延长线于点D.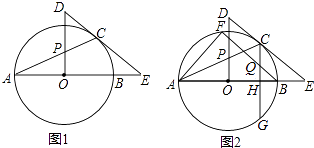
(1)求证:△PCD是等腰三角形;
(2)CG⊥AB于H点,交⊙O于G点,过B点作BF∥EC,交⊙O于点F,交CG于Q点,连接AF,如图2,若sinE= ![]() ,CQ=5,求AF的值.
,CQ=5,求AF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了探究n条直线能把平面最多分成几部分,我们从最简单的情形入手:
①一条直线把平面分成2部分;
②两条直线可把平面最多分成4部分;
③三条直线可把平面最多分成7部分;
④四条直线可把平面最多分成11部分;
……
把上述探究的结果进行整理,列表分析:
直线条数 | 把平面最多 分成的部分数 | 写成和的形式 |
1 | 2 | 1+1 |
2 | 4 | 1+1+2 |
3 | 7 | 1+1+2+3 |
4 | 11 | 1+1+2+3+4 |
… | … | … |
(1)当直线条数为5时,把平面最多分成____部分,写成和的形式:______;
(2)当直线条数为10时,把平面最多分成____部分;
(3)当直线条数为n时,把平面最多分成多少部分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黔东南州某校吴老师组织九(1)班同学开展数学活动,带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,某天在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D处测得电线杆顶端A的仰角为30°,在C处测得电线杆顶端A得仰角为45°,斜坡与地面成60°角,CD=4m,请你根据这些数据求电线杆的高(AB).
(结果精确到1m,参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=2 ![]() ,则这个圆锥底面圆的半径是( )
,则这个圆锥底面圆的半径是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有三张分别标有数字1、2、6的卡片,它们除了数字外完全相同,把卡片背面朝上洗匀,从中任意抽取一张,将上面的数字记为a(不放回),再从中任意抽取一张,将上面的数字记为b,这样的数字a,b能使关于x的一元二次方程x2﹣2(a﹣3)x﹣b2+9=0有两个正根的概率为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).将△AOB绕点O逆时针旋转90°后得到△A1OB1 . 
(1)画出旋转后的△A1OB1 , 点A1的坐标为;
(2)在旋转过程中,点B经过的路径为 ![]() ,求
,求 ![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com