
【题目】某宾馆有50个房间供游客居住,当每个房间每天的定价为180元时,房间会全部住满;当每个房间每天的定价每增加10元时,就会有一个房间空闲.如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用.
(1)若每个房间定价增加40元,则这个宾馆这一天的利润为多少元?
(2)若宾馆某一天获利10640元,则房价定为多少元?
(3)房价定为多少时,宾馆的利润最大?
【答案】
(1)解:若每个房间定价增加40元,则这个宾馆这一天的利润为(180+40﹣20)×(50﹣ ![]() )=9200元
)=9200元
(2)解:设每个房间的定价为a元,
根据题意,得:(a﹣20)(50﹣ ![]() )=10640,
)=10640,
解得:a=300或a=400,
答:若宾馆某一天获利10640元,则房价定为300元或400元
(3)解:设房价增加x元时,利润为w,
则w=(180﹣20+x)(50﹣ ![]() )
)
=﹣ ![]() x2+34x+8000
x2+34x+8000
=﹣ ![]() (x﹣170)2+10890
(x﹣170)2+10890
因而当x=170时,即房价是350元时,利润最大
【解析】(1)根据利润=房价的净利润×入住的房间数可得;(2)设每个房间的定价为a元,根据以上关系式列出方程求解可得;(3)根据(1)中相等关系列出函数解析式,根据函数的性质可得最值情况.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣2x+10与x轴,y轴相交于A,B两点,点C的坐标是(8,4),连接AC,BC.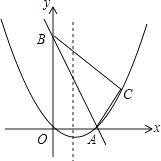
(1)求过O,A,C三点的抛物线的解析式,并判断△ABC的形状;
(2)动点P从点O出发,沿OB以每秒2个单位长度的速度向点B运动;同时,动点Q从点B出发,沿BC以每秒1个单位长度的速度向点C运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为t秒,当t为何值时,PA=QA?
(3)在抛物线的对称轴上,是否存在点M,使以A,B,M为顶点的三角形是等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°. 
(1)求BD的长;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F分别是正方形ABCD的边CD、AD上的点.且CE=DF,AE、BF相交于点O,下列结论:①AE=BF,②AE⊥BF,③AO=OE,④S△AOB=S四边形DEOF中,错误的有 . (只填序号) 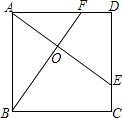
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣1,0),对称轴为直线x=1,给出以下结论:
①abc<0;②b2﹣4ac>0;③9a+3b+c>0;④若B( ![]() ,y1)、C(2,y2)为函数图象上的两点,则y1>y2 ,
,y1)、C(2,y2)为函数图象上的两点,则y1>y2 ,
其中正确的结论是(填写代表正确结论的序号) . 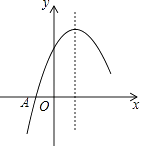
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,小敏利用课余时间制作了一个脸盆架,图2是它的截面图,垂直放置的脸盆与架子的交点为A,B,AB=40cm,脸盆的最低点C到AB的距离为10cm,则该脸盆的半径为cm.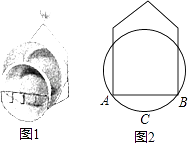
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60m到达C点,测得点B在点C的北偏东60°方向,如图2.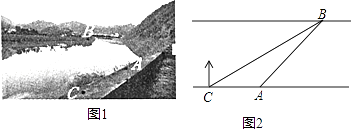
(1)求∠CBA的度数.
(2)求出这段河的宽(结果精确到1m,备用数据 ![]() ≈1.41,
≈1.41, ![]() ≈1.73).
≈1.73).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C:y=x2﹣2x+1的顶点为P,与y轴的交点为Q,点F(1, ![]() ).
).
(1)求点P,Q的坐标;
(2)将抛物线C向上平移得到抛物线C′,点Q平移后的对应点为Q′,且FQ′=OQ′.
①求抛物线C′的解析式;
②若点P关于直线Q′F的对称点为K,射线FK与抛物线C′相交于点A,求点A的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com