
【题目】为了探究n条直线能把平面最多分成几部分,我们从最简单的情形入手:
①一条直线把平面分成2部分;
②两条直线可把平面最多分成4部分;
③三条直线可把平面最多分成7部分;
④四条直线可把平面最多分成11部分;
……
把上述探究的结果进行整理,列表分析:
直线条数 | 把平面最多 分成的部分数 | 写成和的形式 |
1 | 2 | 1+1 |
2 | 4 | 1+1+2 |
3 | 7 | 1+1+2+3 |
4 | 11 | 1+1+2+3+4 |
… | … | … |
(1)当直线条数为5时,把平面最多分成____部分,写成和的形式:______;
(2)当直线条数为10时,把平面最多分成____部分;
(3)当直线条数为n时,把平面最多分成多少部分?
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣1,0),对称轴为直线x=1,给出以下结论:
①abc<0;②b2﹣4ac>0;③9a+3b+c>0;④若B( ![]() ,y1)、C(2,y2)为函数图象上的两点,则y1>y2 ,
,y1)、C(2,y2)为函数图象上的两点,则y1>y2 ,
其中正确的结论是(填写代表正确结论的序号) . 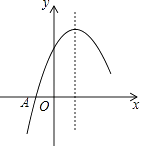
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(﹣2,0),B(2,0),C(3,5).
(1)求过点A,C的直线解析式和过点A,B,C的抛物线的解析式;
(2)求过点A,B及抛物线的顶点D的⊙P的圆心P的坐标;
(3)在抛物线上是否存在点Q,使AQ与⊙P相切,若存在请求出Q点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点C在线段AB上,点M、N分别是AC、BC的中点.(10分)
![]()
(1)若AC=8,CB=6,求线段MN的长;
(2)若点C为线段AB上任意一点,且满足AC+BC=a,请直接写出线段MN的长;
(3)若点C为线段AB延长线上任意一点,且满足AC-CB=b,求线段MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】凯里市某文具店某种型号的计算器每只进价12元,售价20元,多买优惠,优势方法是:凡是一次买10只以上的,每多买一只,所买的全部计算器每只就降价0.1元,例如:某人买18只计算器,于是每只降价0.1×(18﹣10)=0.8(元),因此所买的18只计算器都按每只19.2元的价格购买,但是每只计算器的最低售价为16元.
(1)求一次至少购买多少只计算器,才能以最低价购买?
(2)求写出该文具店一次销售x(x>10)只时,所获利润y(元)与x(只)之间的函数关系式,并写出自变量x的取值范围;
(3)一天,甲顾客购买了46只,乙顾客购买了50只,店主发现卖46只赚的钱反而比卖50只赚的钱多,请你说明发生这一现象的原因;当10<x≤50时,为了获得最大利润,店家一次应卖多少只?这时的售价是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣5(a≠0)与x轴交于点A(﹣5,0)和点B(3,0),与y轴交于点C.
(1)求该抛物线的解析式;
(2)若点E为x轴下方抛物线上的一动点,当S△ABE=S△ABC时,求点E的坐标;
(3)在(2)的条件下,抛物线上是否存在点P,使∠BAP=∠CAE?若存在,求出点P的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线与x轴只有一个交点A(﹣2,0),与y轴交于点B(0,4).
(1)求抛物线对应的函数解析式;
(2)过点B作平行于x轴的直线交抛物线与点C.
①若点M在抛物线的AB段(不含A、B两点)上,求四边形BMAC面积最大时,点M的坐标;
②在平面直角坐标系内是否存在点P,使以P、A、B、C为顶点的四边形是平行四边形,若存在直接写出所有满足条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com