
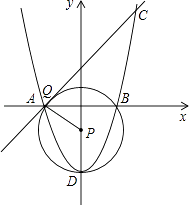
【题目】在平面直角坐标系中,已知点A(﹣2,0),B(2,0),C(3,5).
(1)求过点A,C的直线解析式和过点A,B,C的抛物线的解析式;
(2)求过点A,B及抛物线的顶点D的⊙P的圆心P的坐标;
(3)在抛物线上是否存在点Q,使AQ与⊙P相切,若存在请求出Q点坐标.
【答案】
(1)
解:∵A(﹣2,0),B(2,0);
∴设二次函数的解析式为y=a(x﹣2)(x+2)…①,
把C(3,5)代入①得a=1;
∴二次函数的解析式为:y=x2﹣4;
设一次函数的解析式为:y=kx+b(k≠0)…②
把A(﹣2,0),C(3,5)代入②得 ![]() ,
,
解得 ![]() ,
,
∴一次函数的解析式为:y=x+2
(2)
解:设P点的坐标为(0,Py),
由(1)知D点的坐标为(0,﹣4);
∵A,B,D三点在⊙P上;
∴PB=PD;
∴22+Py2=(﹣4﹣Py)2,
解得:Py=﹣ ![]() ;
;
∴P点的坐标为(0,﹣ ![]() )
)
(3)
解:在抛物线上存在这样的点Q使直线AQ与⊙P相切.
理由如下:设Q点的坐标为(m,m2﹣4);
根据平面内两点间的距离公式得:AQ2=(m+2)2+(m2﹣4)2,PQ2=m2+(m2﹣4+ ![]() )2;
)2;
∵AP= ![]() ,
,
∴AP2= ![]() ;
;
∵直线AQ是⊙P的切线,
∴AP⊥AQ;
∴PQ2=AP2+AQ2,
即:m2+(m2﹣4+ ![]() )2=
)2= ![]() +[(m+2)2+(m2﹣4)2]
+[(m+2)2+(m2﹣4)2]
解得:m1= ![]() ,m2=﹣2(与A点重合,舍去)
,m2=﹣2(与A点重合,舍去)
∴Q点的坐标为( ![]() ,
, ![]() ).
).
【解析】本题考查了二次函数的综合题,涉及的知识点还有利用待定系数法求一次函数的解析式和二次函数的解析式,一元二次方程,是一道综合性较强的题目,但难度不大,要熟练掌握解题思路和方法.(1)利用抛物线和x轴的两个交点坐标,设出抛物线的解析式y=a(x﹣x1)(x﹣x2),代入即可得出抛物线的解析式,再设出直线AC的解析式,利用待定系数法即可得出答案;(2)先求得抛物线的顶点D的坐标,再设点P坐标(0,Py),根据A,B,D三点在⊙P上,得PB=PD,列出关于Py的方程,求解即可得出P点的坐标;(3)假设抛物线上存在这样的点Q使直线AQ与⊙P相切,设Q点的坐标为(m,m2﹣4),根据平面内两点间的距离公式,即可得出关于m的方程,求出m的值,即可得出点Q的坐标.
【考点精析】通过灵活运用确定一次函数的表达式,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法即可以解答此题.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=8cm,BC=16cm,点P从点A出发沿AB边想向点B以2cm/s的速度移动,点Q从点B出发沿BC边向点C以4cm/s的速度移动,如果P、Q同时出发,经过几秒后△PBQ和△ABC相似? 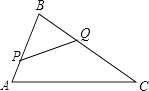
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在⊙O中,AB为直径,C为⊙O上一点.
(1)如图1.过点C作⊙O的切线,与AB的延长线相交于点P,若∠CAB=27°,求∠P的大小;
(2)如图2,D为 ![]() 上一点,且OD经过AC的中点E,连接DC并延长,与AB的延长线相交于点P,若∠CAB=10°,求∠P的大小.
上一点,且OD经过AC的中点E,连接DC并延长,与AB的延长线相交于点P,若∠CAB=10°,求∠P的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AB是⊙O的直径,E是AB延长线上一点,EC切⊙O于点C,OP⊥AO交AC于点P,交EC的延长线于点D.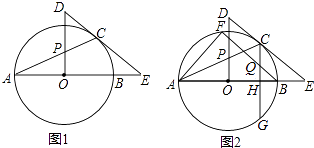
(1)求证:△PCD是等腰三角形;
(2)CG⊥AB于H点,交⊙O于G点,过B点作BF∥EC,交⊙O于点F,交CG于Q点,连接AF,如图2,若sinE= ![]() ,CQ=5,求AF的值.
,CQ=5,求AF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为有效开发海洋资源,保护海洋权益,我国对南海诸岛进行了全面调查,一测量船在A岛测得B岛在北偏西30°,C岛在北偏东15°,航行100海里到达B岛,在B岛测得C岛在北偏东45°,求B,C两岛及A,C两岛的距离( ![]() ≈2.45,结果保留到整数)
≈2.45,结果保留到整数) 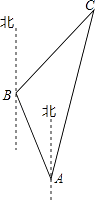
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了探究n条直线能把平面最多分成几部分,我们从最简单的情形入手:
①一条直线把平面分成2部分;
②两条直线可把平面最多分成4部分;
③三条直线可把平面最多分成7部分;
④四条直线可把平面最多分成11部分;
……
把上述探究的结果进行整理,列表分析:
直线条数 | 把平面最多 分成的部分数 | 写成和的形式 |
1 | 2 | 1+1 |
2 | 4 | 1+1+2 |
3 | 7 | 1+1+2+3 |
4 | 11 | 1+1+2+3+4 |
… | … | … |
(1)当直线条数为5时,把平面最多分成____部分,写成和的形式:______;
(2)当直线条数为10时,把平面最多分成____部分;
(3)当直线条数为n时,把平面最多分成多少部分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=2 ![]() ,则这个圆锥底面圆的半径是( )
,则这个圆锥底面圆的半径是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,某学校计划用彩色的地面砖铺设教学楼门前一块矩形操场ABCD的地面.已知这个矩形操场地面的长为100m,宽为80m,图案设计如图所示:操场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都为小正方形的边长,在实际铺设的过程总,阴影部分铺红色地面砖,其余部分铺灰色地面砖. 
(1)如果操场上铺灰色地面砖的面积是铺红色地面砖面积的4倍,那么操场四角的每个小正方形边长是多少米?
(2)如果灰色地面砖的价格为每平方米30元,红色地面砖的价格为每平方米20元,学校现有15万元资金,问这些资金是否能购买所需的全部地面砖?如果能购买所学的全部地面砖,则剩余资金是多少元?如果不能购买所需的全部地面砖,教育局还应该至少给学校解决多少资金?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com