
【题目】如图,已知点C在线段AB上,点M、N分别是AC、BC的中点.(10分)
![]()
(1)若AC=8,CB=6,求线段MN的长;
(2)若点C为线段AB上任意一点,且满足AC+BC=a,请直接写出线段MN的长;
(3)若点C为线段AB延长线上任意一点,且满足AC-CB=b,求线段MN的长.
科目:初中数学 来源: 题型:
【题目】学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为1.6m的小明(AB)的影子BC长是3m,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得HB=6m.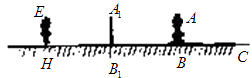
(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置G;
(2)求路灯灯泡的垂直高度GH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的四边相等,且面积为120cm2 , 对角线AC=24cm,则四边形ABCD的周长为( ) 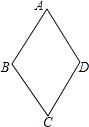
A.52cm
B.40cm
C.39cm
D.26cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为有效开发海洋资源,保护海洋权益,我国对南海诸岛进行了全面调查,一测量船在A岛测得B岛在北偏西30°,C岛在北偏东15°,航行100海里到达B岛,在B岛测得C岛在北偏东45°,求B,C两岛及A,C两岛的距离( ![]() ≈2.45,结果保留到整数)
≈2.45,结果保留到整数) 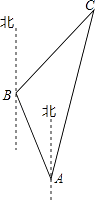
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,AC=BC=2 ![]() ,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是( )
,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是( )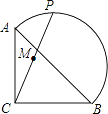
A.![]()
B.π
C.2 ![]()
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了探究n条直线能把平面最多分成几部分,我们从最简单的情形入手:
①一条直线把平面分成2部分;
②两条直线可把平面最多分成4部分;
③三条直线可把平面最多分成7部分;
④四条直线可把平面最多分成11部分;
……
把上述探究的结果进行整理,列表分析:
直线条数 | 把平面最多 分成的部分数 | 写成和的形式 |
1 | 2 | 1+1 |
2 | 4 | 1+1+2 |
3 | 7 | 1+1+2+3 |
4 | 11 | 1+1+2+3+4 |
… | … | … |
(1)当直线条数为5时,把平面最多分成____部分,写成和的形式:______;
(2)当直线条数为10时,把平面最多分成____部分;
(3)当直线条数为n时,把平面最多分成多少部分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,矩形OABC的边OA、OC分别在x轴和y轴上,OC=3,OA=2 ![]() ,D是BC的中点,将△OCD沿直线OD折叠后得到△OGD,延长OG交AB于点E,连接DE,则点G的坐标为 .
,D是BC的中点,将△OCD沿直线OD折叠后得到△OGD,延长OG交AB于点E,连接DE,则点G的坐标为 . 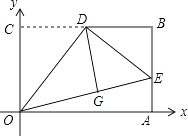
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC为对角线,AC=BC=5,AB=6,AE是△ABC的中线.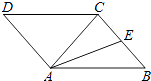
(1)用无刻度的直尺画出△ABC的高CH(保留画图痕迹);
(2)求△ACE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个质地均匀的小正方体,六个面分别标有数字“1”“2”“3”“4”“5”“6”.连续两次抛掷小正方体,观察每次朝上一面的数字.
(1)请用列表格或画树状图的方法列举出两次抛掷的所有可能结果;
(2)求出第二次抛掷的数字大于第一次抛掷的数字的概率;
(3)求两次抛掷的数字之和为5的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com