
【题目】如图,四边形ABCD的四边相等,且面积为120cm2 , 对角线AC=24cm,则四边形ABCD的周长为( ) 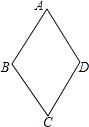
A.52cm
B.40cm
C.39cm
D.26cm
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+mx+m﹣4经过点A(5,﹣5),若抛物线顶点为P.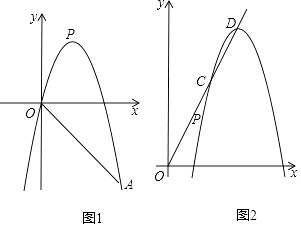
(1)求点P的坐标;
(2)在直线OA上方的抛物线上任取一点M,连接MO、MA,求△MOA的面积取得最大时的点M坐标;
(3)如图1,将原抛物线沿射线OP方向进行平移得到新的抛物线,新抛物线与射线OP交于C、D两点.试问线段CD的长度是否为定值,若是请求出这个定值;若不是请说明理由.(提示:若点C(x1 , y1),D(x2 , y2),则CD的长度d= ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则 ![]() 的值等于 .
的值等于 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点.
![]()
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=acm,其它条件不变,你能猜想MN的长度吗?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的面积为3cm2 , E为BC边上一点,∠BAE=30°,F为AE的中点,过点F作直线分别与AB,DC相交于点M,N.若MN=AE,则AM的长等于 cm.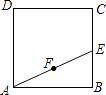
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点C在线段AB上,点M、N分别是AC、BC的中点.(10分)
![]()
(1)若AC=8,CB=6,求线段MN的长;
(2)若点C为线段AB上任意一点,且满足AC+BC=a,请直接写出线段MN的长;
(3)若点C为线段AB延长线上任意一点,且满足AC-CB=b,求线段MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,图形是一种重要的数学语言,它直观形象,能有效地表现一些代数中的数量关系,对几何图形做出代数解释和用几何图形的面积表示代数恒等式是互逆的.课本上由拼图用几何图形的面积来验证了乘法公式,一些代数恒等式也能用这种形式表示,例如(2a+b)(a+b)=2a2+3ab+b2就可以用图①或图②等图形的面积表示.
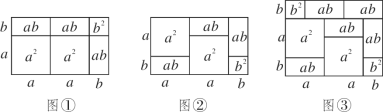
(1)填一填:请写出图③所表示的代数恒等式:______________________________;
(2)画一画:试画出一个几何图形,使它的面积能表示:(a+b)(a+3b)=a2+4ab+3b2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com