
【题目】如图,已知抛物线与x轴只有一个交点A(﹣2,0),与y轴交于点B(0,4).
(1)求抛物线对应的函数解析式;
(2)过点B作平行于x轴的直线交抛物线与点C.
①若点M在抛物线的AB段(不含A、B两点)上,求四边形BMAC面积最大时,点M的坐标;
②在平面直角坐标系内是否存在点P,使以P、A、B、C为顶点的四边形是平行四边形,若存在直接写出所有满足条件的点P的坐标;若不存在,请说明理由.
【答案】
(1)
解:由已知可设抛物线对应函数的解析式为:y=a(x+2)2(a≠0),
∵抛物线与y轴交于点B(0,4)
∴4=a(0+2)2
解得:a=1
∴抛物线对应的解析式为:y=(x+2)2
(2)
解:①如图1中,设点M的坐标为(m,(m+2)2),其中﹣2<m<0,
则N点坐标(m,0).

∵A、B、C是定点,
∴若要四边形BMAC的面积最大,
只要BMA的面积最大即可.
过M做MN⊥x轴于点N,则
S△AOB= ![]() OAOB=
OAOB= ![]() ×2×4=4
×2×4=4
S△AMN= ![]() ANMN=
ANMN= ![]() ×[m﹣(﹣2)]×(m+2)2=
×[m﹣(﹣2)]×(m+2)2= ![]() (m+2)3
(m+2)3
S梯形ONMB= ![]() ON(MN+OB)
ON(MN+OB)
= ![]() ×(﹣m)×[(m+2)2+4]
×(﹣m)×[(m+2)2+4]
=﹣ ![]() (m3+4m2+8m)
(m3+4m2+8m)
∴S△AMB=S△AOB﹣S△AMN﹣S梯形ONMB
=4﹣ ![]() (m+2)3﹣[﹣
(m+2)3﹣[﹣ ![]() (m3+4m2+8m)]
(m3+4m2+8m)]
=﹣m2﹣2m,
当m=﹣1时,S△AMB最大,
∵(﹣1+2)2=1
∴此时点M的坐标为(﹣1,1).
②存在.如图2中,
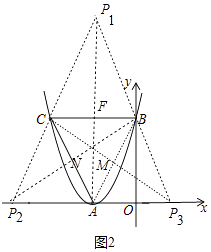
∵四边形ABP1C是平行四边形,
∴FC=FB,AF=FP1,
∵B(0,4),C(﹣4,4),
∴F(﹣2,4),
设P1(x,y),则有 ![]() =﹣2,
=﹣2, ![]() =4,
=4,
∴x=﹣2,y=8,
∴P1(﹣2,8),同法可得P2(﹣6,0),P3(2,0).
所有满足条件的点P的坐标是(2,0)、(﹣6,0)、(﹣2,8)
【解析】(1)由已知可设抛物线对应函数的解析式为:y=a(x+2)2(a≠0),把点B坐标代入求出a即可.(2)①)①如图1中,设点M的坐标为(m,(m+2)2),其中﹣2<m<0,则N点坐标(m,0).若要四边形BMAC的面积最大,只要BMA的面积最大即可,构建二次函数,利用二次函数的性质即可解决问题.(3)有三种情形,先画出图形,利用中点坐标公式一一求解即可.


科目:初中数学 来源: 题型:
【题目】为了探究n条直线能把平面最多分成几部分,我们从最简单的情形入手:
①一条直线把平面分成2部分;
②两条直线可把平面最多分成4部分;
③三条直线可把平面最多分成7部分;
④四条直线可把平面最多分成11部分;
……
把上述探究的结果进行整理,列表分析:
直线条数 | 把平面最多 分成的部分数 | 写成和的形式 |
1 | 2 | 1+1 |
2 | 4 | 1+1+2 |
3 | 7 | 1+1+2+3 |
4 | 11 | 1+1+2+3+4 |
… | … | … |
(1)当直线条数为5时,把平面最多分成____部分,写成和的形式:______;
(2)当直线条数为10时,把平面最多分成____部分;
(3)当直线条数为n时,把平面最多分成多少部分?
查看答案和解析>>
科目:初中数学 来源: 题型:
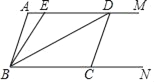
【题目】如图,两条射线AM∥BN,线段CD的两个端点C、D分别在射线BN、AM上,且∠A=∠BCD=108°.E是线段AD上一点(不与点A、D重合),且BD平分∠EBC.
(1)求∠ABC的度数.
(2)请在图中找出与∠ABC相等的角,并说明理由.
(3)若平行移动CD,且AD>CD,则∠ADB与∠AEB的度数之比是否随着CD位置的变化而发生变化?若变化,找出变化规律;若不变,求出这个比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,某学校计划用彩色的地面砖铺设教学楼门前一块矩形操场ABCD的地面.已知这个矩形操场地面的长为100m,宽为80m,图案设计如图所示:操场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都为小正方形的边长,在实际铺设的过程总,阴影部分铺红色地面砖,其余部分铺灰色地面砖. 
(1)如果操场上铺灰色地面砖的面积是铺红色地面砖面积的4倍,那么操场四角的每个小正方形边长是多少米?
(2)如果灰色地面砖的价格为每平方米30元,红色地面砖的价格为每平方米20元,学校现有15万元资金,问这些资金是否能购买所需的全部地面砖?如果能购买所学的全部地面砖,则剩余资金是多少元?如果不能购买所需的全部地面砖,教育局还应该至少给学校解决多少资金?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个质地均匀的小正方体,六个面分别标有数字“1”“2”“3”“4”“5”“6”.连续两次抛掷小正方体,观察每次朝上一面的数字.
(1)请用列表格或画树状图的方法列举出两次抛掷的所有可能结果;
(2)求出第二次抛掷的数字大于第一次抛掷的数字的概率;
(3)求两次抛掷的数字之和为5的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).将△AOB绕点O逆时针旋转90°后得到△A1OB1 . 
(1)画出旋转后的△A1OB1 , 点A1的坐标为;
(2)在旋转过程中,点B经过的路径为 ![]() ,求
,求 ![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某电信部门计划修建一条连接B、C两地的电缆.测量人员在山脚A点测得B、C两地的仰角分别为30°、45°,在B地测得C地的仰角为60°.已知C地比A地高200m,电缆BC至少长多少米(精确到1m)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com