
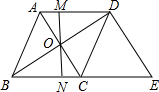
 如图,在菱形ABCD中,对角线AC与BD相交于点O,MN过点O且与边AD、BC分别交于点M和点N.
如图,在菱形ABCD中,对角线AC与BD相交于点O,MN过点O且与边AD、BC分别交于点M和点N.分析 (1)根据四边形ABCD是菱形,判断出AD∥BC,AO=OC,即可推得OM=ON.
(2)首先根据四边形ABCD是菱形,判断出AC⊥BD,AD=BC=AB=6,进而求出BO、BD的值是多少;然后根据DE∥AC,AD∥CE,判断出四边形ACED是平行四边形,求出DE=AC=6,即可求出△BDE的周长是多少.
解答 解:(1)∵四边形ABCD是菱形,
∴AD∥BC,AO=OC,
∴$\frac{OM}{ON}=\frac{AO}{OC}=1$,
∴OM=ON.
(2)∵四边形ABCD是菱形,
∴AC⊥BD,AD=BC=AB=6,
∴BO=$\sqrt{{AB}^{2}{-AO}^{2}}=\sqrt{{6}^{2}{-(8÷2)}^{2}}$=2$\sqrt{5}$,
∴$BD=2BO=2×2\sqrt{5}=4\sqrt{5}$,
∵DE∥AC,AD∥CE,
∴四边形ACED是平行四边形,
∴DE=AC=8,
∴△BDE的周长是:
BD+DE+BE
=BD+AC+(BC+CE)
=4$\sqrt{5}$+8+(6+6)
=20$+4\sqrt{5}$
即△BDE的周长是20$+4\sqrt{5}$.
点评 (1)此题主要考查了菱形的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:菱形是在平行四边形的前提下定义的,首先它是平行四边形,但它是特殊的平行四边形,特殊之处就是“有一组邻边相等”,因而就增加了一些特殊的性质和不同于平行四边形的判定方法.
(2)此题还考查了三角形的周长的含义以及求法,以及勾股定理的应用,要熟练掌握.


科目:初中数学 来源: 题型:解答题
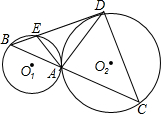 如图,已知⊙O1、⊙O2外切于点A,过点A的直线交⊙O1于B,交⊙O2于C,过点B作直线BD与⊙O1⊙O2分别相交于E,D,连接AE,AD,DC,若AE:AD=ED:DC.
如图,已知⊙O1、⊙O2外切于点A,过点A的直线交⊙O1于B,交⊙O2于C,过点B作直线BD与⊙O1⊙O2分别相交于E,D,连接AE,AD,DC,若AE:AD=ED:DC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
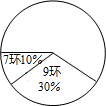 第17届亚洲运动会于2014年9月19日-10月4日在韩国仁川举行,中国射击队对这次仁川亚运会非常重视,在一次选拔赛中,运动员甲10次射击成绩的统计表和扇形统计图如下:
第17届亚洲运动会于2014年9月19日-10月4日在韩国仁川举行,中国射击队对这次仁川亚运会非常重视,在一次选拔赛中,运动员甲10次射击成绩的统计表和扇形统计图如下:| 命中环数 | 10 | 9 | 8 | 7 |
| 命中次数 | 4 | 3 | 2 | ,1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知在⊙O中,AB是弦,半径OC⊥AB,垂足为点D,要使四边形OACB为菱形,还需要添加一个条件,这个条件可以是( )
如图,已知在⊙O中,AB是弦,半径OC⊥AB,垂足为点D,要使四边形OACB为菱形,还需要添加一个条件,这个条件可以是( )| A. | AD=BD | B. | OD=CD | C. | ∠CAD=∠CBD | D. | ∠OCA=∠OCB |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
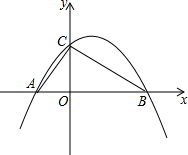 如图,已知抛物线y=ax2+bx+c经过A(-2,0),B(4,0),C(0,3)三点.
如图,已知抛物线y=ax2+bx+c经过A(-2,0),B(4,0),C(0,3)三点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com