
����Ŀ����ͼ1����Rt��ABC�У���C��90����AC��BC����D��E�ֱ��ڱ�AC��BC�ϣ�CD��CE������AE����F��H��G�ֱ�ΪDE��AE��AB���е�����FH��HG
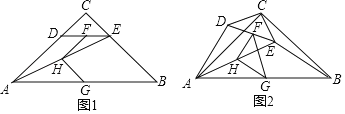
��1���۲����ͼ1�У��߶�FH��GH��������ϵ���� ����λ�ù�ϵ���� ��
��2��̽��֤��������CDE�Ƶ�C˳ʱ�뷽����ת��ͼ2��λ�ã�����AD��AE��BE�ж���FHG����״����˵������
��3����չ���죺����CDE�Ƶ�C��ƽ����������ת����CD��4��AC��8����ֱ��д����FHG��������ֵ
���𰸡���1��FH��GH��FH��HG����2����FGP�ǵ���ֱ�������Σ����ɼ���������3��18
��������
��1��ֱ�����������ε���λ�߶����ó�FH��GH���ٽ��������ε���ǵ����ʼ��ɵó���FHG��90�������ɵó����ۣ�
��2���������֤��CAD�ա�CBE���ɵá�CAD����CBE��AD��BE��������������λ�߶�������֤HG��HF��HF��AD��HG��BE�����ݽǵ�������ϵ�����GHF��90��������֤��FGH�ǵ���ֱ�������Σ�
��3��������ɵ�S��HGF�����![]() HG2��HG���ʱ����FGH������D��AC���ӳ����ϣ����������FGH��������ֵ��
HG2��HG���ʱ����FGH������D��AC���ӳ����ϣ����������FGH��������ֵ��
�⣺��1����AC��BC��CD��CE��
��AD��BE��
�ߵ�F��DE���е㣬��H��AE���е㣬
��FH��![]() AD��
AD��
�ߵ�G��AB���е㣬��H��AE���е㣬
��GH��![]() BE��
BE��
��FH��GH��
�ߵ�F��DE���е㣬��H��AE���е㣬
��FH��AD��
���FHE����CAE
�ߵ�G��AB���е㣬��H��AE���е㣬
��GH��BE��
���AGH����B��
�ߡ�C��90����AC��BC��
���BAC����B��45����
�ߡ�EGH����B+��BAE��
���FHG����FHE+��EHG����CAE+��B+��BAE����B+��BAC��90����
��FH��HG��
�ʴ�Ϊ��FH��GH��FH��HG��
��2����FGP�ǵ���ֱ��������
���ɣ�����ת֪����ACD����BCE��
��AC��BC��CD��CE��
���CAD�ա�CBE��SAS����
���CAD����CBE��AD��BE��
�������ε���λ�ߵã�HG��![]() BE��HF��
BE��HF��![]() AD��
AD��
��HG��HF��
���FGH�ǵ��������Σ�
�������ε���λ�ߵã�HG��BE��
���AGH����ABE��
�������ε���λ�ߵã�HF��AD��
���FHE����DAE��
�ߡ�EHG����BAE+��AGH����BAE+��ABE��
���GHF����FHE+��EHG
����DAE+��BAE+��ABE
����BAD+��ABE
����BAC+��CAD+��ABC����CBE
����CBA+��CAB��
�ߡ�ACB��90����AC��BC��
���CBA����CAB��45����
���GHF��90����
���FGH�ǵ���ֱ�������Σ�
��3���ɣ�2��֪����FGH�ǵ���ֱ�������Σ�HG��HF��![]() AD��
AD��
��S��HGF��![]() HG2��
HG2��
��HG���ʱ����FGH������
���D��AC���ӳ����ϣ�
��CD��4��AC��8
��AD��AC+CD��12��
��HG��![]() ��12��6��
��12��6��
��S��PGF�����![]() HG2��18��
HG2��18��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����죬�ˣ�1���չ���ʵ�������һС�黨90Ԫ���߲������г������˻ƹϺ����ӹ�40kg�����߲��г�ȥ�����ƹϺ����ӵ���������������ۼ������ʾ��
Ʒ�� | �ƹ� | ���� |
������/��Ԫ/kg�� | 2.4 | 2 |
���ۼ�/��Ԫ/kg�� | 3.6 | 2.8 |
��1���ƹϺ����Ӹ������˶���kg��
��2����С�鵱��������Щ�ƹϺ����ӿ�����Ǯ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��x�ύ�ڵ�A��B����
��x�ύ�ڵ�A��B����![]() �ύ�ڵ�C������C��CD��x�ᣬ�������ߵĶԳ����ڵ�D������BD����֪��A����Ϊ��-1��0����
�ύ�ڵ�C������C��CD��x�ᣬ�������ߵĶԳ����ڵ�D������BD����֪��A����Ϊ��-1��0����

��1����������ߵĽ���ʽ��
��2��������COBD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
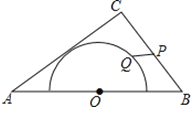
����Ŀ����![]() �У�
��![]() ��
��![]() ���Ա�
���Ա�![]() ���е�
���е�![]() ΪԲ�ģ�����Բ��
ΪԲ�ģ�����Բ��![]() ���У���
���У���![]() �ֱ��DZ�
�ֱ��DZ�![]() �Ͱ�Բ�ϵĶ��㣬����
�Ͱ�Բ�ϵĶ��㣬����![]() ����
����![]() �������ֵ����Сֵ�ĺ���__________��
�������ֵ����Сֵ�ĺ���__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪һ�κ���![]() ��ͼ����x�ᡢy��ֱ���
��ͼ����x�ᡢy��ֱ���![]() ���㣬�뷴��������
���㣬�뷴��������![]() ��ͼ��ֱ���
��ͼ��ֱ���![]() ���㣬��
���㣬��![]() ��
��![]() ��
��
![]() ��һ�κ���
��һ�κ���![]() �뷴��������
�뷴��������![]() �Ľ���ʽ��
�Ľ���ʽ��
![]() ֱ��д��
ֱ��д��![]() ʱ�Ա���x��ȡֵ��Χ��
ʱ�Ա���x��ȡֵ��Χ��
![]() ����
����![]() ��y�����˶�����
��y�����˶�����![]() ��ֵ���ʱ��ֱ��д��P������꣮
��ֵ���ʱ��ֱ��д��P������꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
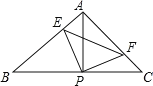
����Ŀ����ͼ����֪��ABC�У�AB=AC����BAC=90�㣬ֱ�ǡ�EPF�Ķ���P��BC�е㣬����PE��PF�ֱ�AB��AC�ڵ�E��F������EPF�ڡ�ABC����ƽ�����ƶ���Pת��ʱ(��E����A��B�غ�)�����������ĸ����ۣ�����PFA�ա�PEB��EF=AP����PEF�ǵ���ֱ����������S�ı���AEPF![]() S��ABC������������ʼ����ȷ��______��
S��ABC������������ʼ����ȷ��______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x��һԪ���η���x2+��k��5��x+1��k=0������kΪ������
��1����֤������kΪ��ֵ�������������������ʵ������
��2����ԭ���̵�һ������3����һ��С��3����k���������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ij��2016����ҵ��ˮ��x���֣������Ӧ����ˮ��y��Ԫ��֮��ĺ�����ϵ��ͼ��

��1����x��50ʱ����y����x�ĺ�����ϵʽ��
��2����ij��ҵ2016��10�·ݵ�ˮ��Ϊ620Ԫ�������ҵ2016��10�·ݵ���ˮ����
��3��Ϊ������ҵ��Լ��ˮ��������2017��1�¿�ʼ������ˮ������80�ֵ���ҵ������ˮ�����ѣ��涨������ҵ����ˮ��x����80�֣������2016���շѱ���ȡˮ���⣬����80�ֵIJ���ÿ��������![]() Ԫ����ˮ�����ѣ���ij��ҵ2017��3�·ݵ�ˮ�Ѻ���ˮ�����ѹ�600Ԫ���������ҵ3�·ݵ���ˮ����
Ԫ����ˮ�����ѣ���ij��ҵ2017��3�·ݵ�ˮ�Ѻ���ˮ�����ѹ�600Ԫ���������ҵ3�·ݵ���ˮ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���֪OΪ����ԭ�㣬��A��3��0����B��0.4�����Ե�AΪ��ת���ģ�����ABO˳ʱ����ת������ACD������ת��Ϊ������ABOΪ����

��I ����ͼ��������ת���Dǡ������AB����ʱ�����D�����ꣻ
��II����ͼ��������ת������BC��x��ʱ����������֮���������ϵ��
��III������ת��������AOD=��ʱ����ֱ��CD�Ľ���ʽ��ֱ��д��������ɣ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com