
【题目】如图所示,△OAB中,OA=OB=10,∠AOB=80°,以点O为圆心,6为半径的优弧![]() 分别交OA、OB于点M、N.
分别交OA、OB于点M、N.
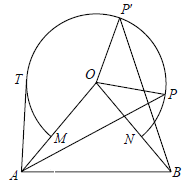
(1)点P在右半弧上(∠BOP是锐角),将OP绕点O逆时针旋转80°得OP′. 求证:AP = BP′;
(2)点T在左半弧上,若AT与弧![]() 相切于点T,求点T到OA的距离;
相切于点T,求点T到OA的距离;
(3)设点Q在优弧![]() 上,当△AOQ的面积最大时,直接写出∠BOQ的度数.
上,当△AOQ的面积最大时,直接写出∠BOQ的度数.
【答案】(1)根据已知得出∠AOP=∠BOP′,从进而由SAS得出△AOP≌△BOP′,即可得出答案。
(2)![]()
(3)10°或170°
【解析】试题分析:(1)首先根据已知得出∠AOP=∠BOP′,进而得出△AOP≌△BOP′,即可得出答案;
(2)利用切线的性质得出∠ATO=90°,再利用勾股定理求出AT的长,进而得出TH的长即可得出答案;
(3)当OQ⊥OA时,△AOQ面积最大,且左右两半弧上各存在一点分别求出即可.
试题解析:(1)如图1,

∵∠AOP=∠AOB+∠BOP=80°+∠BOP,
∠BOP′=∠POP′+∠BOP=80°+∠BOP,
∴∠AOP=∠BOP′,
∵在△AOP和△BOP′中

∴△AOP≌△BOP′(SAS),
∴AP=BP′;
(2)如图1,连接OT,过点T作TH⊥OA于点H,
∵AT与弧MN相切,
∴∠ATO=90°,
∴AT=![]() =
=![]() =8,
=8,
∵![]() ×OA×TH=
×OA×TH=![]() ×AT×OT,
×AT×OT,
即![]() ×10×TH=
×10×TH=![]() ×8×6,
×8×6,
解得:TH=![]() ,即点T到OA的距离为
,即点T到OA的距离为![]() ;
;
(3)如图2,当OQ⊥OA时,△AOQ的面积最大;

理由:∵OQ⊥OA,
∴QO是△AOQ中最长的高,则△AOQ的面积最大,
∴∠BOQ=∠AOQ+∠AOB=90°+80°=170°,
当Q点在优弧MN右侧上,
∵OQ⊥OA,
∴QO是△AOQ中最长的高,则△AOQ的面积最大,
∴∠BOQ=∠AOQ-∠AOB=90°-80°=10°,
综上所述:当∠BOQ的度数为10°或170°时,△AOQ的面积最大.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案科目:初中数学 来源: 题型:
【题目】如图,E,F是四边形ABCD的对角线AC上两点,AF=CE,DF=BE,DF∥BE. 求证: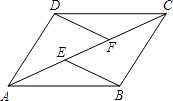
(1)△AFD≌△CEB;
(2)四边形ABCD是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科技馆对学生参观实行优惠,个人票为每张6元,另有团体票可售,票价45元,每票最多限10人入馆参观.
(1)如果参观的学生人数36人,至少应付多少元?
(2)如果参观的学生人数为48人,至少应付多少元?
(3)如果参观的学生人数为一个两位数 ![]() (a表示十位上的数字,b表示个位上的数字),用含a、b的代数式表示至少应付给科技馆的总金额.
(a表示十位上的数字,b表示个位上的数字),用含a、b的代数式表示至少应付给科技馆的总金额.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请根据图中提供的信息,回答下列问题: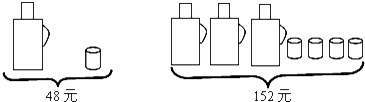
(1)一个水瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的水瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定:这两种商品都打八折;乙商场规定:买一个水瓶赠送两个水杯,另外购买的水杯按原价卖.若某单位想要买5个水瓶和20个水杯,请问选择哪家商场购买更合算,并说明理由.(必须在同一家购买)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】包括中国志愿者王跃在内的6名志愿者踏上了为期12480小时的“火星之旅”.将12480用科学记数法表示应为( )
A. 12.48×103 B. 0.1248×105 C. 1.248×104 D. 1.248×103
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自开展“学生每天锻炼1小时”活动后,我市某中学根据学校实际情况,决定开设A:毽子,B:篮球,C:跑步,D:跳绳四种运动项目.为了了解学生最喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如图统计图.请结合图中信息解答下列问题:
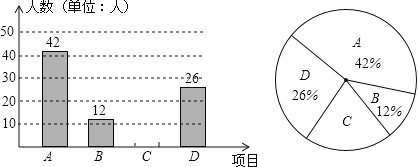
(1)该校本次调查中,共调查了多少名学生?
(2)请将两个统计图补充完整;
(3)在本次调查的学生中随机抽取1人,他喜欢“跑步”的概率有多大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com