练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知⊙O的半径为10cm，OP＝8cm，则点P和⊙O的位置关系是（　　）

    A.点P在圆内B.点P在圆上C.点P在圆外D.无法判断

    【答案】A

    【解析】

    比较OP与圆的半径的大小，然后根据点与圆的位置关系判断点P和⊙O的位置关系；

    解：∵点P到圆心的距离OP＝8cm，小于⊙O的半径10cm，

    ∴点P在在圆内．

    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】为了解外来务工子女就学情况，某校对七年级各班级外来务工子女的人数情况进行了统计，发现各班级中外来务工子女的人数有1名、2名、3名、4名、5名、6名共六种情况，并制成如下两幅统计图：

    (1)求该校七年级平均每个班级有多少名外来务工子女?并将该条形统计图补充完整；

    (2)学校决定从只有2名外来务工子女的这些班级中，任选两名进行生活资助，请用列表法或画树状图的方法，求出所选两名外来务工子女来自同一个班级的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校开展课外体育活动，决定开设A：篮球、B：乒乓球、C：踢毽子、D：跑步四种活动项目．为了解学生最喜欢哪一种活动项目（每人只选取一种），随机抽取了部分学生进行调查，并将调查结果绘成如甲、乙所示的统计图，请你结合图中信息解答下列问题．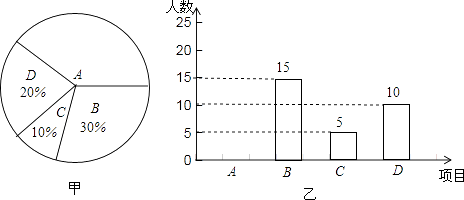
    （1）样本中最喜欢A项目的人数所占的百分比为 ， 其所在扇形统计图中对应的圆心角度数是度；
    （2）请把条形统计图补充完整；
    （3）若该校有学生1000人，请根据样本估计全校最喜欢踢毽子的学生人数约是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】四边形一条对角线所在直线上的点，如果到这条对角线的两端点的距离不相等，但到另一对角线的两个端点的距离相等，则称这点为这个四边形的准等距点．如图，点P为四边形ABCD对角线AC所在直线上的一点，PD=PB，PA≠PC，则点P为四边形ABCD的准等距点．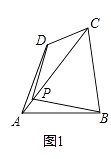
    （1）如图2，画出菱形ABCD的一个准等距点．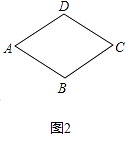
    （2）如图3，作出四边形ABCD的一个准等距点（尺规作图，保留作图痕迹，不要求写作法）．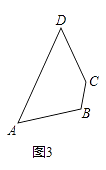
    （3）如图4，在四边形ABCD中，P是AC上的点，PA≠PC，延长BP交CD于点E，延长DP交BC于点F，且∠CDF=∠CBE，CE=CF．求证：点P是四边形ABCD的准等距点．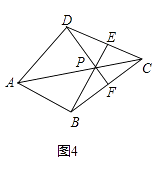

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若顺次连接四边形ABCD各边的中点所得四边形是矩形，则四边形ABCD一定满足（ ）
    A.对角线相等
    B.对角线互相平分
    C.对角线互相垂直
    D.对角线相等且相互平分

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】-6的相反数等于__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数y＝（x﹣5）2+7的最小值是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB=90°，AC=BC=1，将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE，点B经过的路径为弧BD，则图中阴影部分的面积是________.

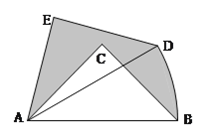
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，△OAB中，OA=OB=10，∠AOB=80°，以点O为圆心，6为半径的优弧分别交OA、OB于点M、N.

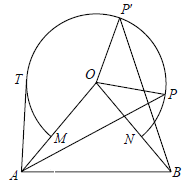
    （1）点P在右半弧上（∠BOP是锐角），将OP绕点O逆时针旋转80°得OP′. 求证：AP = BP′；

    （2）点T在左半弧上，若AT与弧相切于点T，求点T到OA的距离；

    （3）设点Q在优弧上，当△AOQ的面积最大时，直接写出∠BOQ的度数.

    查看答案和解析>>

    同步练习册答案