
����Ŀ���ı���һ���Խ�������ֱ���ϵĵ㣬����������Խ��ߵ����˵�ľ��벻��ȣ�������һ�Խ��ߵ������˵�ľ�����ȣ�������Ϊ����ı��ε��Ⱦ�㣮��ͼ����PΪ�ı���ABCD�Խ���AC����ֱ���ϵ�һ�㣬PD=PB��PA��PC�����PΪ�ı���ABCD���Ⱦ�㣮 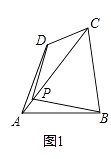
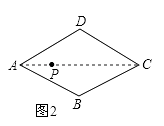
��1����ͼ2����������ABCD��һ���Ⱦ�㣮 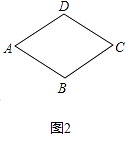
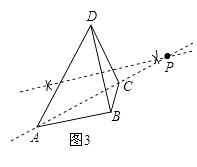
��2����ͼ3�������ı���ABCD��һ���Ⱦ�㣨�߹���ͼ��������ͼ�ۼ�����Ҫ��д�������� 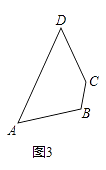
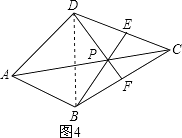
��3����ͼ4�����ı���ABCD�У�P��AC�ϵĵ㣬PA��PC���ӳ�BP��CD�ڵ�E���ӳ�DP��BC�ڵ�F���ҡ�CDF=��CBE��CE=CF����֤����P���ı���ABCD���Ⱦ�㣮 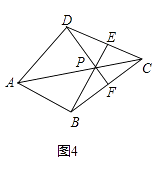
���𰸡�
��1���⣺��ͼ2����P��Ϊ�����㣮
��2���⣺��ͼ3����P��Ϊ������
��3���⣺֤��������DB��
�ڡ�DCF���BCE�У� 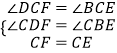 ��
��
���DCF�ա�BCE��AAS����
��CD=CB��
���CDB=��CBD��
���PDB=��PBD��
��PD=PB��
��PA��PC
���P���ı���ABCD���Ⱦ��
����������1���������ε����ʣ������ζԽ������ҳ��������������һ�㼴�ɣ���2�����Խ���BD�Ĵ�ֱƽ����������һ�Խ���AC�ཻ�ڵ�P�������߶δ�ֱƽ�����ϵĵ㵽�߶����˵�ľ�����ȿɵõ�P��Ϊ������Ⱦ�㣻��3������BD�������á��ǽDZߡ�֤����DCF�͡�BCEȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�CD=CB���ٸ��ݵȱ߶ԵȽǵ����ʿɵá�CDB=��CBD���Ӷ��õ���PDB=��PBD��Ȼ����ݵȽǶԵȱߵ����ʿɵ�PD=PB�������Ⱦ��Ķ��弴�ɵ�֤��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c����A����3.0����C��0��4������B���������ϣ�CB��x�ᣬ��ABƽ�֡�CAO��
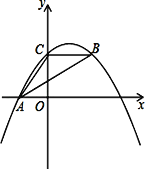
��1���������ߵĽ���ʽa��b��c��
��2���߶�AB����һ����P������P��y���ƽ���ߣ����������ڵ�Q�����߶�PQ�����ֵ��
��3�������ߵĶԳ������Ƿ���ڵ�M��ʹ��ABM����ABΪֱ�DZߵ�ֱ�������Σ�������������M���ꣻ��������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���� ![]() �У�
�У� ![]() ������Ϊ
������Ϊ ![]() ����
���� ![]() ��
�� ![]() �ϣ�
�ϣ� ![]() ������Ϊ
������Ϊ ![]() .
.
��1��![]() ��
�� ![]() ƽ����Ϊʲô��
ƽ����Ϊʲô��
��2����� ![]() ����
���� ![]() ����
���� ![]() �Ķ���.
�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����48λͬѧ����һ����ѧ����У�����ֻȡ������ͳ����ɼ������Ƴ�Ƶ���ֲ�ֱ��ͼ��������ʾ��������50.5�ֵ�100.5��֮��ķ����ֳ�5�飬�����10�֣��ݰ����ʾƵ������ͼ��ʾ�������ҵ�С���εĸ߶ȱ���1��3��6��4��2������ͼ��֪�����з�����70.5��80.5֮��������ǣ�������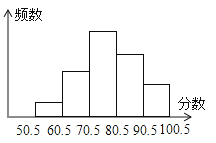
A.9
B.18
C.12
D.6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ȼ�������ֵ��
��a2b+��3ab2��a2b����2��2ab2��a2b��������a��b����|a+1|+��b+2��2=0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��O�İ뾶Ϊ10cm��OP��8cm�����P�͡�O��λ�ù�ϵ�ǣ�������
A.��P��Բ��B.��P��Բ��C.��P��Բ��D.���ж�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���y=kx��k��y��x���������С������ͼ���� ��
A. ��һ���� B. �ڶ����� C. �������� D. ��������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com