
【题目】先化简,再求值:
﹣a2b+(3ab2﹣a2b)﹣2(2ab2﹣a2b),其中a、b满足|a+1|+(b+2)2=0.
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】毕达哥拉斯学派对”数”与”形”的巧妙结合作了如下研究:
名称及图形 | 三角形数 | 正方形数 | 五边形数 | 六边形数 |
|
|
|
| |
第一层几何点数 | 1 | 1 | 1 | 1 |
第二层几何点数 | 2 | 3 | 4 | 5 |
第三层几何点数 | 3 | 5 | 7 | 9 |
… | … | … | … | … |
第六层几何点数 | ||||
… | … | … | … | … |
第n层几何点数 |
请写出第六层各个图形的几何点数,并归纳出第n层各个图形的几何点数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级教材在图形与几何部分给出了五条基本事实,在《证明》一章中我们从两条基本事实出发,把前面得到的平行线相关性质进行了严格的证明,体会了数学的公里化思想.请完成下列证明活动:
(1)活动 ![]() .利用基本事实证明:“两直线平行,同位角相等”.(在括号内填上相应的基本事实)
.利用基本事实证明:“两直线平行,同位角相等”.(在括号内填上相应的基本事实)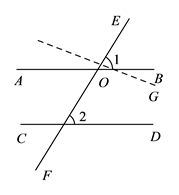
已知:如图,直线 ![]() 、
、 ![]() 被直线
被直线 ![]() 所截,
所截, ![]() .
.
求证: ![]() .
.
证明:假设 ![]() ,则可以过点
,则可以过点 ![]() 作
作 ![]() .
.
∵ ![]() ,
,
∴ ![]() ().
().
∴过 ![]() 点存在两条直线
点存在两条直线 ![]() 、
、 ![]() 两条直线与
两条直线与 ![]() 平行,这与基本事实()矛盾.
平行,这与基本事实()矛盾.
∴假设不成立.
∴ ![]() .
.
(2)活动 ![]() .利用刚刚证明的“两直线平行,同位角相等”证明“两直线平行,同旁内角互补”.(要求画图,写出已知、求证并写出证明过程)
.利用刚刚证明的“两直线平行,同位角相等”证明“两直线平行,同旁内角互补”.(要求画图,写出已知、求证并写出证明过程)
已知:.
求证:.
证明: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知抛物线y=x2+bx+c与x轴交于A、B两点(点A在点B左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.
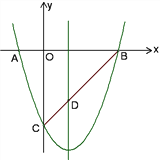
(1)求抛物线的函数表达式;
(2)求直线BC的函数表达式;
(3)点E为y轴上一动点,CE的垂直平分线交CE于点F,交抛物线于P、Q两点,且点P在第三象限.
①当线段PQ ![]() 时,求tan∠CED的值;
时,求tan∠CED的值;
②当以C、D、E为顶点的三角形是直角三角形时,请直接写出点P的坐标.
(参考公式:抛物线![]() 的顶点坐标是
的顶点坐标是 )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形一条对角线所在直线上的点,如果到这条对角线的两端点的距离不相等,但到另一对角线的两个端点的距离相等,则称这点为这个四边形的准等距点.如图,点P为四边形ABCD对角线AC所在直线上的一点,PD=PB,PA≠PC,则点P为四边形ABCD的准等距点. 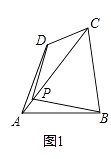
(1)如图2,画出菱形ABCD的一个准等距点. 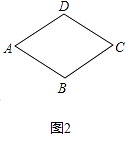
(2)如图3,作出四边形ABCD的一个准等距点(尺规作图,保留作图痕迹,不要求写作法). 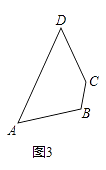
(3)如图4,在四边形ABCD中,P是AC上的点,PA≠PC,延长BP交CD于点E,延长DP交BC于点F,且∠CDF=∠CBE,CE=CF.求证:点P是四边形ABCD的准等距点. 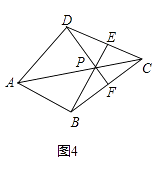
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中真命题的个数是( )
①用四舍五入法对0.05049取近似值为0.050(精确到0.001);
②若代数式![]() 有意义,则x的取值范围是x≤-
有意义,则x的取值范围是x≤-![]() 且x≠-2;
且x≠-2;
③点P(2,-3)关于x轴的对称点为P,(-2,- 3);
④月球距离地球表面约为384000000米,这个距离用科学记数法表示为3.84×108米.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于下列图形:①等边三角形;②矩形;③平行四边形;④菱形;⑤正八边形;⑥圆.其中既是轴对称图形,又是中心对称图形的是______.(填写图形的相应编号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com