
【题目】如图,抛物线y=ax2+bx+c经过A(﹣3.0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO.
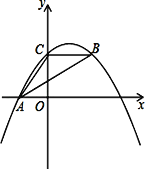
(1)求抛物线的解析式a,b,c;
(2)线段AB上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;
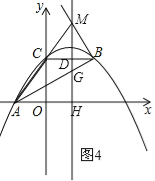
(3)抛物线的对称轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在求出点M坐标;如果不存在,说明理由.
【答案】(1)抛物线的解析式为y=﹣![]() x2+
x2+![]() x+4;
x+4;
(2)线段PQ的最大值为![]() ;
;
(3)符合要求的点M的坐标为(![]() ,9)和(
,9)和(![]() ,﹣11).
,﹣11).
【解析】试题分析:(1)如图1,易证BC=AC,从而得到点B的坐标,然后运用待定系数法求出二次函数的解析式;
(2)如图2,运用待定系数法求出直线AB的解析式.设点P的横坐标为t,从而可以用t的代数式表示出PQ的长,然后利用二次函数的最值性质就可解决问题;
(3)由于AB为直角边,分别以∠BAM=90°(如图3)和∠ABM=90°(如图4)进行讨论,通过三角形相似建立等量关系,就可以求出点M的坐标.
试题解析:(1)如图1,
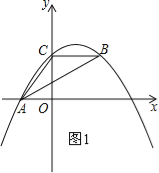
∵A(﹣3,0),C(0,4),
∴OA=3,OC=4.
∵∠AOC=90°,
∴AC=5.
∵BC∥AO,AB平分∠CAO,
∴∠CBA=∠BAO=∠CAB.
∴BC=AC.
∴BC=5.
∵BC∥AO,BC=5,OC=4,
∴点B的坐标为(5,4).
∵A(﹣3.0)、C(0,4)、B(5,4)在抛物线y=ax2+bx+c上,
∴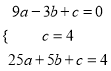
解得: 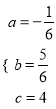
∴抛物线的解析式为y=﹣![]() x2+
x2+![]() x+4;
x+4;
(2)如图2,
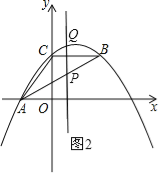
设直线AB的解析式为y=mx+n,
∵A(﹣3.0)、B(5,4)在直线AB上,
∴![]()
解得: ![]()
∴直线AB的解析式为y=![]() x+
x+![]() .
.
设点P的横坐标为t(﹣3≤t≤5),则点Q的横坐标也为t.
∴yP=![]() t+
t+![]() ,yQ=﹣
,yQ=﹣![]() t2+
t2+![]() t+4.
t+4.
∴PQ=yQ﹣yP=﹣![]() t2+
t2+![]() t+4﹣(
t+4﹣(![]() t+
t+![]() )
)
=﹣![]() t2+
t2+![]() t+4﹣
t+4﹣![]() t﹣
t﹣![]()
=﹣![]() t2+
t2+![]() +
+![]()
=﹣![]() (t2﹣2t﹣15)
(t2﹣2t﹣15)
=﹣![]() [(t﹣1)2﹣16]
[(t﹣1)2﹣16]
=﹣![]() (t﹣1)2+
(t﹣1)2+![]() .
.
∵﹣![]() <0,﹣3≤1≤5,
<0,﹣3≤1≤5,
∴当t=1时,PQ取到最大值,最大值为![]() .
.
∴线段PQ的最大值为![]() ;
;
(3)①当∠BAM=90°时,如图3所示.
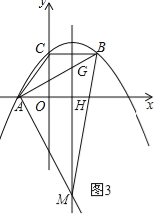
抛物线的对称轴为x=﹣![]() =﹣
=﹣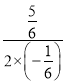 =
=![]() .
.
∴xH=xG=xM=![]() .
.
∴yG=![]() ×
×![]() +
+![]() =
=![]() .
.
∴GH=![]() .
.
∵∠GHA=∠GAM=90°,
∴∠MAH=90°﹣∠GAH=∠AGM.
∵∠AHG=∠MHA=90°,∠MAH=∠AGM,
∴△AHG∽△MHA.
∴![]() .
.
∴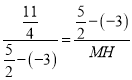 .
.
解得:MH=11.
∴点M的坐标为(![]() ,﹣11).
,﹣11).
②当∠ABM=90°时,如图4所示.
∵∠BDG=90°,BD=5﹣![]() =
=![]() ,DG=4﹣
,DG=4﹣![]() =
=![]() ,
,
∴BG=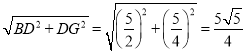 .
.
同理:AG=![]() .
.
∵∠AGH=∠MGB,∠AHG=∠MBG=90°,
∴△AGH∽△MGB.
∴![]() .
.
∴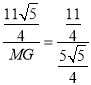 .
.
解得:MG=![]() .
.
∴MH=MG+GH=![]() +
+![]() =9.
=9.
∴点M的坐标为(![]() ,9).
,9).
综上所述:符合要求的点M的坐标为(![]() ,9)和(
,9)和(![]() ,﹣11).
,﹣11).


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
【题目】某商家预测一种应季衬衫能畅销市场,就用13 200元购进了一批这种衬衫,面市后果然供不应求,商家又用28 800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完利润率不低于25%(不考虑其他因素),那么每件衬衫的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】毕达哥拉斯学派对”数”与”形”的巧妙结合作了如下研究:
名称及图形 | 三角形数 | 正方形数 | 五边形数 | 六边形数 |
|
|
|
| |
第一层几何点数 | 1 | 1 | 1 | 1 |
第二层几何点数 | 2 | 3 | 4 | 5 |
第三层几何点数 | 3 | 5 | 7 | 9 |
… | … | … | … | … |
第六层几何点数 | ||||
… | … | … | … | … |
第n层几何点数 |
请写出第六层各个图形的几何点数,并归纳出第n层各个图形的几何点数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解外来务工子女就学情况,某校对七年级各班级外来务工子女的人数情况进行了统计,发现各班级中外来务工子女的人数有1名、2名、3名、4名、5名、6名共六种情况,并制成如下两幅统计图:
(1)求该校七年级平均每个班级有多少名外来务工子女?并将该条形统计图补充完整;
(2)学校决定从只有2名外来务工子女的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名外来务工子女来自同一个班级的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形一条对角线所在直线上的点,如果到这条对角线的两端点的距离不相等,但到另一对角线的两个端点的距离相等,则称这点为这个四边形的准等距点.如图,点P为四边形ABCD对角线AC所在直线上的一点,PD=PB,PA≠PC,则点P为四边形ABCD的准等距点. 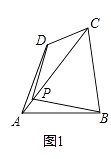
(1)如图2,画出菱形ABCD的一个准等距点. 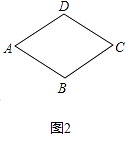
(2)如图3,作出四边形ABCD的一个准等距点(尺规作图,保留作图痕迹,不要求写作法). 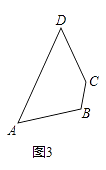
(3)如图4,在四边形ABCD中,P是AC上的点,PA≠PC,延长BP交CD于点E,延长DP交BC于点F,且∠CDF=∠CBE,CE=CF.求证:点P是四边形ABCD的准等距点. 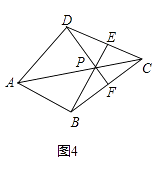
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com