练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】若实数x满足等式（x+4）3=﹣27，则x= ．

    【答案】-7
    【解析】解：∵（﹣3）3=﹣27， ∴x+4=﹣3，
    解得x=7．
    所以答案是：﹣7．
    【考点精析】认真审题，首先需要了解立方根(如果一个数的立方等于a，那么这个数就叫做a 的立方根（或a 的三次方根）；一个正数有一个正的立方根；一个负数有一个负的立方根；零的立方根是零)．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

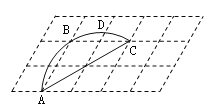
    【题目】如图，15个形状大小完全相同的菱形组成网格，菱形的顶点称为格点. 已知菱形的一个角为60°，A、B、C都在格点上，点D在过A、B、C三点的圆弧上，若E也在格点上，且∠AED=∠ACD，则cos∠AEC=________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料：
    现规定一种运算： =ad﹣bc．
    例如： =1×4﹣2×3=4﹣6=﹣2； =4x﹣（﹣2）×3=4x+6．
    按照这种规定的运算，请解答下列问题：
    （1） =（只填结果）；
    （2）已知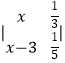： =1．求x的值．（写出解题过程）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将一张0.1毫米厚的白纸对折8次后，其厚度为毫米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一元二次方程4x2+5x＝81，二次项系数为_____，一次项为_____，常数项为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

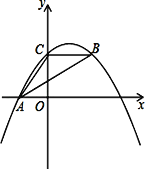
    【题目】如图，抛物线y=ax2+bx+c经过A（﹣3.0）、C（0，4），点B在抛物线上，CB∥x轴，且AB平分∠CAO．

    （1）求抛物线的解析式a，b，c；

    （2）线段AB上有一动点P，过点P作y轴的平行线，交抛物线于点Q，求线段PQ的最大值；

    （3）抛物线的对称轴上是否存在点M，使△ABM是以AB为直角边的直角三角形？如果存在求出点M坐标；如果不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知Rt△ABC中，∠ABC=90°，先把△ABC绕点B顺时针旋转90°至△DBE后，再把△ABC沿射线平移至△FEG，DE、FG相交于点H．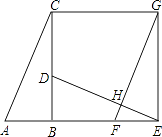
    （1）判断线段DE、FG的位置关系，并说明理由；
    （2）连结CG，求证：四边形CBEG是正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，菱形ABCD的对角线AC与BD交于点O，AC=6，BD=8．动点E从点B出发，沿着B﹣A﹣D在菱形ABCD的边上运动，运动到点D停止．点F是点E关于BD的对称点，EF交BD于点P，若BP=x，△OEF的面积为y，则y与x之间的函数图象大致为（　　）

    A. B.

    C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某班有48位同学，在一次数学检测中，分数只取整数，统计其成绩，绘制出频数分布直方图（横半轴表示分数，把50.5分到100.5分之间的分数分成5组，组距是10分，纵半轴表示频数）如图所示，从左到右的小矩形的高度比是1：3：6：4：2，则由图可知，其中分数在70.5～80.5之间的人数是（　　）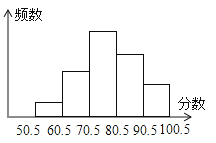

    A.9
    B.18
    C.12
    D.6

    查看答案和解析>>

    同步练习册答案