
【题目】如图,在 ![]() 中,
中, ![]() ,垂足为
,垂足为 ![]() ,点
,点 ![]() 在
在 ![]() 上,
上, ![]() ,垂足为
,垂足为 ![]() .
.
(1)![]() 与
与 ![]() 平行吗?为什么?
平行吗?为什么?
(2)如果 ![]() ,且
,且 ![]() ,求
,求 ![]() 的度数.
的度数.
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案科目:初中数学 来源: 题型:
【题目】为了解外来务工子女就学情况,某校对七年级各班级外来务工子女的人数情况进行了统计,发现各班级中外来务工子女的人数有1名、2名、3名、4名、5名、6名共六种情况,并制成如下两幅统计图:
(1)求该校七年级平均每个班级有多少名外来务工子女?并将该条形统计图补充完整;
(2)学校决定从只有2名外来务工子女的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名外来务工子女来自同一个班级的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级教材在图形与几何部分给出了五条基本事实,在《证明》一章中我们从两条基本事实出发,把前面得到的平行线相关性质进行了严格的证明,体会了数学的公里化思想.请完成下列证明活动:
(1)活动 ![]() .利用基本事实证明:“两直线平行,同位角相等”.(在括号内填上相应的基本事实)
.利用基本事实证明:“两直线平行,同位角相等”.(在括号内填上相应的基本事实)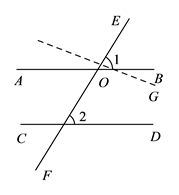
已知:如图,直线 ![]() 、
、 ![]() 被直线
被直线 ![]() 所截,
所截, ![]() .
.
求证: ![]() .
.
证明:假设 ![]() ,则可以过点
,则可以过点 ![]() 作
作 ![]() .
.
∵ ![]() ,
,
∴ ![]() ().
().
∴过 ![]() 点存在两条直线
点存在两条直线 ![]() 、
、 ![]() 两条直线与
两条直线与 ![]() 平行,这与基本事实()矛盾.
平行,这与基本事实()矛盾.
∴假设不成立.
∴ ![]() .
.
(2)活动 ![]() .利用刚刚证明的“两直线平行,同位角相等”证明“两直线平行,同旁内角互补”.(要求画图,写出已知、求证并写出证明过程)
.利用刚刚证明的“两直线平行,同位角相等”证明“两直线平行,同旁内角互补”.(要求画图,写出已知、求证并写出证明过程)
已知:.
求证:.
证明: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校开展课外体育活动,决定开设A:篮球、B:乒乓球、C:踢毽子、D:跑步四种活动项目.为了解学生最喜欢哪一种活动项目(每人只选取一种),随机抽取了部分学生进行调查,并将调查结果绘成如甲、乙所示的统计图,请你结合图中信息解答下列问题. 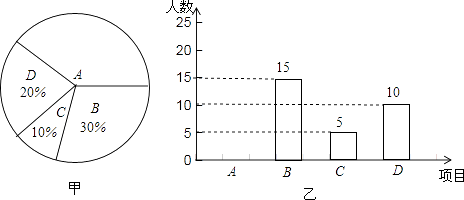
(1)样本中最喜欢A项目的人数所占的百分比为 , 其所在扇形统计图中对应的圆心角度数是度;
(2)请把条形统计图补充完整;
(3)若该校有学生1000人,请根据样本估计全校最喜欢踢毽子的学生人数约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形一条对角线所在直线上的点,如果到这条对角线的两端点的距离不相等,但到另一对角线的两个端点的距离相等,则称这点为这个四边形的准等距点.如图,点P为四边形ABCD对角线AC所在直线上的一点,PD=PB,PA≠PC,则点P为四边形ABCD的准等距点. 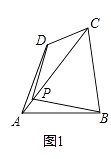
(1)如图2,画出菱形ABCD的一个准等距点. 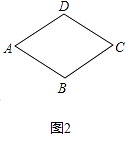
(2)如图3,作出四边形ABCD的一个准等距点(尺规作图,保留作图痕迹,不要求写作法). 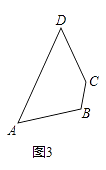
(3)如图4,在四边形ABCD中,P是AC上的点,PA≠PC,延长BP交CD于点E,延长DP交BC于点F,且∠CDF=∠CBE,CE=CF.求证:点P是四边形ABCD的准等距点. 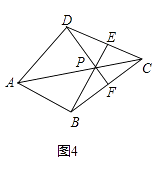
查看答案和解析>>
科目:初中数学 来源: 题型:
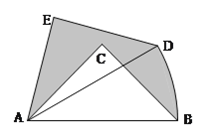
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为弧BD,则图中阴影部分的面积是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com