
���� �ѵ�һ�����̱��α�ʾ��3x-y������ڶ����������3x+4y��ֵ���������x��y��ֵ����Ϊԭ������Ľ⣮
��� �⣺$\left\{\begin{array}{l}{6x-2y=3��}\\{��3x-y����3x+4y��=6��}\end{array}\right.$��
�ɢٵã�3x-y=$\frac{3}{2}$�ۣ�
�Ѣ۴���ڵã�$\frac{3}{2}$��3x+4y��=6��
��ã�3x+4y=4��
�ٽⷽ����$\left\{\begin{array}{l}{6x-2y=3}\\{3x+4y=4}\end{array}\right.$�ã�$\left\{\begin{array}{l}{x=\frac{2}{3}}\\{y=\frac{1}{2}}\end{array}\right.$��
��ԭ������Ľ�Ϊ$\left\{\begin{array}{l}{x=\frac{2}{3}}\\{y=\frac{1}{2}}\end{array}\right.$��
���� ���⿼���˽��Ԫһ�η����飬��������Ԫ��˼�룬��Ԫ�ķ����У�������Ԫ����Ӽ���Ԫ����


 Сѧ������ҵϵ�д�
Сѧ������ҵϵ�д� ��ʿһ��ȫͨϵ�д�
��ʿһ��ȫͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
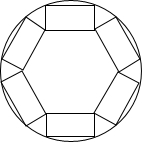 ��ͼΪһ���뾶Ϊ4m��Բ�ι㳡�����з���������Ϊ1m�ij�������ʱ̯λ����Щ̯λ�������������ڹ㳡���ϣ������������������̯λ�Ķ��㣬��ÿ��������̯λ�ij�Ϊ$\frac{-\sqrt{3}+3\sqrt{7}}{2}$m��
��ͼΪһ���뾶Ϊ4m��Բ�ι㳡�����з���������Ϊ1m�ij�������ʱ̯λ����Щ̯λ�������������ڹ㳡���ϣ������������������̯λ�Ķ��㣬��ÿ��������̯λ�ij�Ϊ$\frac{-\sqrt{3}+3\sqrt{7}}{2}$m���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -8 | B�� | -6 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 45�� | B�� | 60�� | C�� | 90�� | D�� | 120�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com