
分析 先分别求出①②③④的结果,发现的规律①=1;②=1+2;③=1+2+3;④=1+2+3+4.以此类推,$\sqrt{{1}^{3}+{2}^{3}+{3}^{3}+…+2{0}^{3}}$=1+2+3+4+…+20=210.
解答 解:$\sqrt{{1}^{3}}$=1,
$\sqrt{{2}^{3}{+1}^{3}}$=1+2,
$\sqrt{{1}^{3}{+2}^{3}{+3}^{3}}$=1+2+3,
$\sqrt{{1}^{3}{+2}^{3}{+3}^{3}{+4}^{3}}$=1+2+3+4,
…
$\sqrt{{1}^{3}+{2}^{3}+{3}^{3}+…+2{0}^{3}}$=1+2+3+4+…+20=210.
点评 此题主要考查了学生的分析,总结归纳的能力,要会从题中数据的特点找到规律,并利用规律解题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
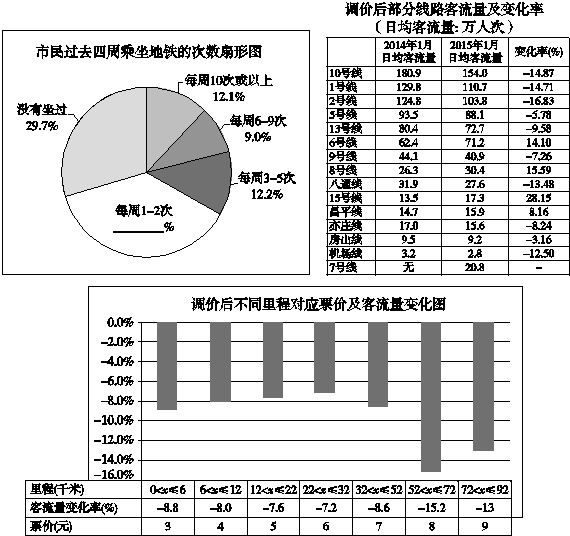
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
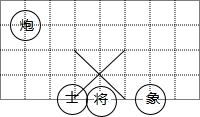 如图,若在象棋盘上建立直角坐标系,使“将”位于点(0,-1),“象”位于(2,-1),则“炮”位于点( )
如图,若在象棋盘上建立直角坐标系,使“将”位于点(0,-1),“象”位于(2,-1),则“炮”位于点( )| A. | (-3,2) | B. | (-4,3) | C. | (-3,0) | D. | (1,-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com