
【题目】已知:如图,在矩形ABCD中,Ab=6cm,BC=8cm,对角线AC,BD交于点0.点P从点A出发,沿方向匀速运动,速度为1cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度为1cm/s;当一个点停止运动时,另一个点也停止运动.连接PO并延长,交BC于点E,过点Q作QF∥AC,交BD于点F.设运动时间为t(s)(0<t<6),解答下列问题:
(1)当t为何值时,△AOP是等腰三角形?
(2)设五边形OECQF的面积为S(cm2),试确定S与t的函数关系式;
(3)在运动过程中,是否存在某一时刻t,使S五边形S五边形OECQF:S△ACD=9:16?若存在,求出t的值;若不存在,请说明理由;
(4)在运动过程中,是否存在某一时刻t,使OD平分∠COP?若存在,求出t的值;若不存在,请说明理由.

【答案】(1)t为![]() 或5;(2)
或5;(2)![]() ;(3)t=
;(3)t=![]() ;(4)t=2.88.
;(4)t=2.88.
【解析】
试题分析:(1)根据矩形的性质和勾股定理得到AC=10,①当AP=PO=t,如图1,过P作PM⊥AO,根据相似三角形的性质得到AP=t=![]() ,②当AP=AO=t=5,于是得到结论;
,②当AP=AO=t=5,于是得到结论;
(2)作EH⊥AC于H,QM⊥AC于M,DN⊥AC于N,交QF于G,根据全等三角形的性质得到CE=AP=t,根据相似三角形的性质表示出EH,根据相似三角形的性质表示出QM,FQ,根据图形的面积即可得到结论;
(3)根据题意列方程得到t的值,于是得到结论;
(4)由角平分线的性质得到DM的长,根据勾股定理得到ON的长,由三角形的面积公式表示出OP,根据勾股定理列方程即可得到结论.
试题解析:(1)∵在矩形ABCD中,Ab=6cm,BC=8cm,∴AC=10,①当AP=PO=t,如图1,过P作PM⊥AO,∴AM=![]() AO=
AO=![]() ,∵∠PMA=∠ADC=90°,∠PAM=∠CAD,∴△APM∽△ADC,∴
,∵∠PMA=∠ADC=90°,∠PAM=∠CAD,∴△APM∽△ADC,∴![]() ,∴AP=t=
,∴AP=t=![]() ,②当AP=AO=t=5,∴当t为
,②当AP=AO=t=5,∴当t为![]() 或5时,△AOP是等腰三角形;
或5时,△AOP是等腰三角形;
(2)作EH⊥AC于H,QM⊥AC于M,DN⊥AC于N,交QF于G,在△APO与△CEO中,∵∠PAO=∠ECO,AO=OC,∠AOP=∠COE,∴△AOP≌△COE,∴CE=AP=t,∵△CEH∽△ABC,∴![]() ,∴EH=
,∴EH=![]() ,∵DN=
,∵DN=![]() =
=![]() ,∵QM∥DN,∴△CQM∽△CDN,∴
,∵QM∥DN,∴△CQM∽△CDN,∴![]() ,即
,即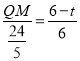 ,∴QM=
,∴QM=![]() ,∴DG=
,∴DG=![]() =
=![]() ,∵FQ∥AC,∴△DFQ∽△DOC,∴
,∵FQ∥AC,∴△DFQ∽△DOC,∴![]() ,∴FQ=
,∴FQ=![]() ,∴S五边形OECQF=S△OEC+S四边形OCQF=
,∴S五边形OECQF=S△OEC+S四边形OCQF=![]() =
=![]() ,∴S与t的函数关系式为
,∴S与t的函数关系式为![]() ;
;
(3)存在,∵S△ACD=![]() ×6×8=24,∴S五边形OECQF:S△ACD=(
×6×8=24,∴S五边形OECQF:S△ACD=(![]() ):24=9:16,解得t=
):24=9:16,解得t=![]() ,t=0,(不合题意,舍去),∴t=
,t=0,(不合题意,舍去),∴t=![]() 时,S五边形S五边形OECQF:S△ACD=9:16;
时,S五边形S五边形OECQF:S△ACD=9:16;
(4)如图3,过D作DM⊥AC于M,DN⊥AC于N,∵∠POD=∠COD,∴DM=DN=![]() ,∴ON=OM=
,∴ON=OM=![]() =
=![]() ,∵OPDM=3PD,∴OP=
,∵OPDM=3PD,∴OP=![]() ,∴PM=
,∴PM=![]() ,∵
,∵![]() ,∴
,∴![]() ,解得:t≈15(不合题意,舍去),t≈2.88,∴当t=2.88时,OD平分∠COP.
,解得:t≈15(不合题意,舍去),t≈2.88,∴当t=2.88时,OD平分∠COP.


科目:初中数学 来源: 题型:
【题目】关于体育选考项目统计图
项目 | 频数 | 频率 |
A | 80 | b |
B | c | 0.3 |
C | 20 | 0.1 |
D | 40 | 0.2 |
合计 | a | 1 |

(1)求出表中a,b,c的值,并将条形统计图补充完整. 表中a= , b= , c= .
(2)如果有3万人参加体育选考,会有多少人选择篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解题:
你知道为什么任何无限循环小数都可以写成分数形式吗?下面的解答过程会告诉你原因和方法.
(1)阅读下列材料:
问题:利用一元一次方程将 ![]() 化成分数.
化成分数.
设 ![]() .
.
由 ![]() ,可知
,可知 ![]() ,
,
即 ![]() .(请你体会将方程两边都乘以10起到的作用)
.(请你体会将方程两边都乘以10起到的作用)
可解得 ![]() ,即
,即 ![]() .
.
填空:将 ![]() 直接写成分数形式为 .
直接写成分数形式为 .
(2)请仿照上述方法把小数 ![]() 化成分数,要求写出利用一元一次方程进行解答的过程.
化成分数,要求写出利用一元一次方程进行解答的过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图①,若∠AOC=30°,求∠DOE的度数;
(2)在图①中,若∠AOC= ![]() ,直接写出∠DOE的度数(用含
,直接写出∠DOE的度数(用含 ![]() 的代数式表示);
的代数式表示);
(3)将图①中的∠DOC绕顶点O顺时针旋转至图②的位置,探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△A′B′C′关于直线m对称。
(1)结合图形指出对称点.
(2)连接A、A′,直线m与线段AA′有什么关系?
(3)延长线段AC与A′C′,它们的交点与直线m有怎样的关系?其它对应线段(或其延长线)的交点呢?你发现了什么规律,请叙述出来与同伴交流。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com