
如图,已知直线AB: 与抛物线
与抛物线 交于A、B两点,
交于A、B两点,
(1)直线AB总经过一个定点C,请直接写出点C坐标;
(2)当 时,在直线AB下方的抛物线上求点P,使△ABP的面积等于5;
时,在直线AB下方的抛物线上求点P,使△ABP的面积等于5;
(3)若在抛物线上存在定点D使∠ADB=90°,求点D到直线AB的最大距离.

(1)(-2,4);(2)(-2,2)或(1,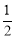 );(3)
);(3)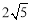 .
.
【解析】
试题分析:(1)要求定点的坐标,只需寻找一个合适x,使得y的值与k无关即可.
(2)只需联立两函数的解析式,就可求出点A、B的坐标.设出点P的横坐标为a,运用割补法用a的代数式表示△APB的面积,然后根据条件建立关于a的方程,从而求出a的值,进而求出点P的坐标.
(3)设点A、B、D的横坐标分别为m、n、t,从条件∠ADB=90°出发,可构造k型相似,从而得到m、n、t的等量关系,然后利用根与系数的关系就可以求出t,从而求出点D的坐标.由于直线AB上有一个定点C,容易得到DC长就是点D到AB的最大距离,只需构建直角三角形,利用勾股定理即可解决问题.
试题解析:(1)∵当x=-2时,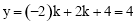 ,
,
∴直线AB:y=kx+2k+4必经过定点(-2,4).
∴点C的坐标为(-2,4).
(2)∵ ,
,
∴直线AB的解析式为 .
.
联立 ,解得:
,解得: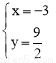 或
或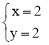 .
.
∴点A的坐标为(-3,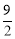 ),点B的坐标为(2,2).
),点B的坐标为(2,2).
如答图1,过点P作PQ∥y轴,交AB于点Q,过点A作AM⊥PQ,垂足为M,过点B作BN⊥PQ,垂足为N.
设点P的横坐标为a,则点Q的横坐标为a.
∴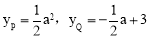 .
.
∵点P在直线AB下方,∴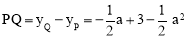 .
.
∵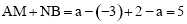 ,
,
∴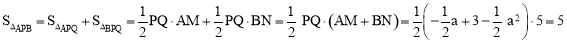 ,
,
整理得: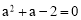 ,解得:
,解得: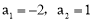 .
.
当 时,
时,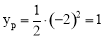 .此时点P的坐标为(-2,2).
.此时点P的坐标为(-2,2).
当a=1时,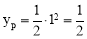 .此时点P的坐标为(1,
.此时点P的坐标为(1,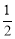 ).
).
∴符合要求的点P的坐标为(-2,2)或(1,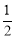 ).
).

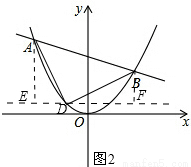
(3)如答图2,过点D作x轴的平行线EF,作AE⊥EF,垂足为E,作BF⊥EF,垂足为F.
∵AE⊥EF,BF⊥EF,∴∠AED=∠BFD=90°.
∵∠ADB=90°,∴∠ADE=90°-∠BDF=∠DBF.
∵∠AED=∠BFD,∠ADE=∠DBF,∴△AED∽△DFB.∴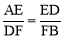 .
.
设点A、B、D的横坐标分别为m、n、t,
则点A、B、D的纵坐标分别为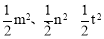 ,
,
∴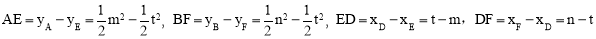 .
.
∴ ,化简得:
,化简得: .
.
∵点A、B是直线AB: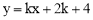 与抛物线
与抛物线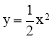 交点,
交点,
∴m、n是方程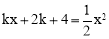 即
即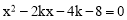 两根.∴
两根.∴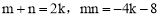 .
.
∴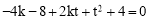 ,即
,即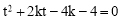 ,即
,即 .
.
∴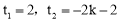 (舍).
(舍).
∴定点D的坐标为(2,2).
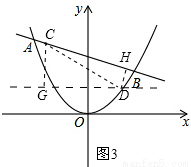
如答图3,过点D作x轴的平行线DG,
过点C作CG⊥DG,垂足为G,
∵点C(-2,4),点D(2,2),∴CG=4-2=2,DG=2-(-2)=4.
∵CG⊥DG,∴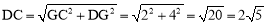 .
.
过点D作DH⊥AB,垂足为H,如答图3所示,
∴DH≤DC.∴DH≤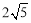 .
.
∴当DH与DC重合即DC⊥AB时,
点D到直线AB的距离最大,最大值为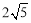 .
.
∴点D到直线AB的最大距离为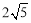 .
.
考点:1.二次函数综合题;2. 因式分解法解一元二次方程;3.根与系数的关系;4.勾股定理;5.相似三角形的判定和性质;6.分类思想的应用.


科目:初中数学 来源:2014年初中毕业升学考试(湖南岳阳卷)数学(解析版) 题型:选择题
下列计算正确的是( )
A.2a+5a=7a B.2x﹣x=1 C.3+a=3a D.x2•x3=x6
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖北武汉卷)数学(解析版) 题型:解答题
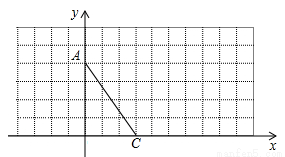
如图,在直角坐标系中,A(0,4)、C(3,0),
(1)① 画出线段AC关于y轴对称线段AB;
② 将线段CA绕点C顺时针旋转一个角,得到对应线段CD,使得AD∥x轴,请画出线段CD;
(2)若直线y=kx平分(1)中四边形ABCD的面积,请直接写出实数k的值.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖北武汉卷)数学(解析版) 题型:填空题
如图,一个转盘被分成7个相同的扇形,颜色分别为红黄绿三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),则指针指向红色的概率为 .

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖北宜昌卷)数学(解析版) 题型:解答题
“低碳生活,绿色出行”是我们倡导的一种生活方式,有关部门抽样调查了某单位员工上下班的交通方式,绘制了如下统计图:
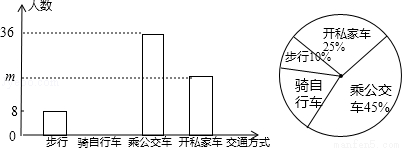
(1)填空:样本中的总人数为 ;开私家车的人数m= ;扇形统计图中“骑自行车”所在扇形的圆心角为 度;
(2)补全条形统计图;
(3)该单位共有2000人,积极践行这种生活方式,越来越多的人上下班由开私家车改为骑自行车.若步行,坐公交车上下班的人数保持不变,问原来开私家车的人中至少有多少人改为骑自行车,才能使骑自行车的人数不低于开私家车的人数?
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江舟山卷)数学(解析版) 题型:选择题
2013年12月15日,我国“玉兔号”月球车顺利抵达月球表面.月球离地球平均距离是384 400 000米,数据384 400 000用科学记数法表示为( )
(A)3.844×108 (B)3.844×107 (C)3.844×106 (D)38.44×106
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com