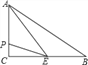
【题目】如图，在△ABC中，∠C=90°，BC=8cm，AC=6cm，点E是BC的中点，动点P从A点出发，先以每秒2cm的速度沿A→C运动，然后以1cm/s的速度沿C→B运动．若设点P运动的时间是t秒，那么当t=_____________，△APE的面积等于6．
【答案】1.5, 5，9
【解析】分析：分为两种情况讨论：当点P在AC上时：当点P在BC上时，根据三角形的面积公式建立方程求出其解即可．
详解：如图1，当点P在AC上．∵△ABC中，∠C=90°，BC=8cm，AC=6cm，点E是BC的中点，∴CE=4，AP=2t．
∵△APE的面积等于6，∴S△APE=
APCE=AP×4=6．∵AP=3，∴t=1.5．
如图2，当点P在BC上．∵E是DC的中点，∴BE=CE=4．
∵BP=2t﹣8，PC=6﹣（2t﹣8）=14﹣2t，∴S=EPAC=EP×6=6，∴EP=2，∴t=3+4﹣2=5或t=3+4+2=9．
总上所述，当t=1.5或5或9时，△APE的面积会等于6．故答案为：1.5或5或9．
应用题天天练四川大学出版社系列答案科目：初中数学 来源： 题型：
【题目】 在锐角三角形ABC中，∠A=50°，则∠B的范围是( )
A.0°＜∠B＜90°B.40°＜∠B＜130°C.40°≤∠B≤90°D.40°＜∠B＜90°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列说法正确的是（ ）
A. 要了解某公司生产的100万只灯泡的使用寿命，可以采用抽样调查的方法
B. 4位同学的数学期末成绩分别为100、95、105、110，则这四位同学数学期末成绩的中位数为100
C. 甲乙两人各自跳远10次，若他们跳远成绩的平均数相同，甲乙跳远成绩的方差分别为0.51和0.62
D. 某次抽奖活动中，中奖的概率为
表示每抽奖50次就有一次中奖
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知AB是⊙O的直径，PB是⊙O的切线，C是⊙O上的点，AC∥OP，M是直径AB上的动点，A与直线CM上的点连线距离的最小值为d，B与直线CM上的点连线距离的最小值为f．
（1）求证：PC是⊙O的切线；
（2）设OP=
AC，求∠CPO的正弦值；
（3）设AC=9，AB=15，求d+f的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商店用1000元人民币购进水果销售，过了一段时间，又用2400元人民币购进这种水果，所购数量是第一次购进数量的2倍，但每千克的价格比第一次购进的贵了2元．
（1）该商店第一次购进水果多少千克？
（2）假设该商店两次购进的水果按相同的标价销售，最后剩下的20千克按标价的五折优惠销售．若两次购进水果全部售完，利润不低于950元，则每千克水果的标价至少是多少元？
注：每千克水果的销售利润等于每千克水果的销售价格与每千克水果的购进价格的差，两批水果全部售完的利润等于两次购进水果的销售利润之和．
查看答案和解析>>
科目：初中数学 来源： 题型：
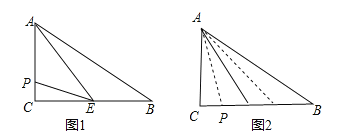
【题目】如图，在四边形ABCD中，∠ABC＝30°，∠ADC＝60°，AD＝DC，连结AC、BD．在四边形ABCD的外部以BC为一边作等边△BCE，连结AE．
（1）求证：BD＝AE；
（2）若AB＝3，BC＝4，求BD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
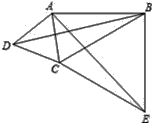
【题目】如图所示，E、F分别为线段AC上的两个点，且DE⊥AC于点E，BF⊥AC于点F，若AB=CD，AE=CF，BD交AC于点M．
（1）试猜想DE与BF的关系，并证明你的结论；
（2）求证：MB=MD．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是一艘轮船和一艘快艇沿相同路线从甲港出发行驶到乙港的过程中路程
y随时间x变化的图象．根据图象解答下列问题：
(1)在轮船和快艇中，哪一艘的速度较快?
(2)当时间x在什么范围内时，快艇在轮船的后面?当时间x在什么范围内时，快艇在轮船的前面?
(3)快艇出发多长时间后赶上轮船?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com