
���� ��1����������·ݼ��ֵ���ÿ̨�ۼ�mԪ�����ݽ������·ݵĵ����ۼ۱�ȥ��ͬ��ÿ̨����1000Ԫ�����������ͬ�����ĵ��ԣ�ȥ�����۶�Ϊ10��Ԫ���������۶�ֻ��8��Ԫ�����з�����⣮
��2���蹺����x̨��������Ϊ��15-x��̨�����ݡ��ò�����4.8��Ԫ���ʽ������ֵ��Թ�15̨���г�����ʽ�飮
��� �⣺��1����������·ݼ��ֵ���ÿ̨�ۼ�ΪmԪ��
$\frac{100000}{100+m}$=$\frac{80000}{m}$��
m=4000
���飺m=4000ʱ��m��1000+m����0��
m=4000��ԭ��ʽ���̵Ľ⣮
�𣺽������·ݵ��ۼ�Ϊ4000Ԫ��
��2���蹺����x̨��������Ϊ��15-x��̨���������
$\left\{\begin{array}{l}{3500+3000��15-x����50000}\\{3500+3000��15-x����48000}\end{array}\right.$��
���x��6��
�����ٹ������ֵ���6̨��
���� ���⿼���˷�ʽ���̵�Ӧ�ã�һԪһ�β���ʽ���Ӧ�ã����÷�ʽ���̽�Ӧ����ʱ��һ����Ŀ�л���������ȹ�ϵ����ʱҪ������Ŀ��Ҫ��������⣬ѡ�����е�һ����ȹ�ϵ��Ϊ�з��̵����ݣ�����һ����������δ֪����


 ��ʦ����ָ���ο�ʱϵ�д�
��ʦ����ָ���ο�ʱϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
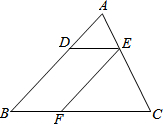 ��ͼ����֪�ڡ�ABC�У���D��E��F�ֱ��DZ�AB��AC��BC�ϵĵ㣬DE��BC��EF��AB����AD��DB=4��7����ôCF��CB���ڣ�������
��ͼ����֪�ڡ�ABC�У���D��E��F�ֱ��DZ�AB��AC��BC�ϵĵ㣬DE��BC��EF��AB����AD��DB=4��7����ôCF��CB���ڣ�������| A�� | 7��11 | B�� | 4��8 | C�� | 4��7 | D�� | 3��7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
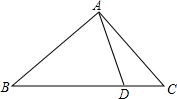 ��ͼ��D�ǡ�ABCһ��BC��һ�㣬����AD��ʹ��ABC�ס�DBA�������ǣ�������
��ͼ��D�ǡ�ABCһ��BC��һ�㣬����AD��ʹ��ABC�ס�DBA�������ǣ�������| A�� | AC��BC=AD��BD | B�� | AC��BC=AB��AD | C�� | AB2=CD•BC | D�� | AB2=BD•BC |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
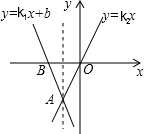 ��ͼ��ֱ��y=k1x+b������A��-1��-2���͵�B��-2��0����ֱ��y=k2x������A�����Ԫһ�η�����$\left\{\begin{array}{l}{y={k}_{1}x+b}\\{y={k}_{2}x}\end{array}\right.$�Ľ�Ϊ$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$������ʽk2x��k1x+b��0�Ľ⼯Ϊx��-1��
��ͼ��ֱ��y=k1x+b������A��-1��-2���͵�B��-2��0����ֱ��y=k2x������A�����Ԫһ�η�����$\left\{\begin{array}{l}{y={k}_{1}x+b}\\{y={k}_{2}x}\end{array}\right.$�Ľ�Ϊ$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$������ʽk2x��k1x+b��0�Ľ⼯Ϊx��-1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
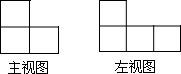 ��ͼ���ɴ�С��ͬ��С��������ɵļ����������ͼ������ͼ����ô�������������С������ĸ������Ϊ��������
��ͼ���ɴ�С��ͬ��С��������ɵļ����������ͼ������ͼ����ô�������������С������ĸ������Ϊ��������| A�� | 7 | B�� | 8 | C�� | 9 | D�� | 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com