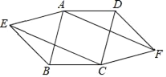
【题目】如图，四边形ABCD是平行四边形，分别以AB，CD为边向外作等边△ABE和△CDF，连接AF，CE．求证：四边形AECF为平行四边形．
【答案】见解析.
【解析】
由平行四边形的性质可得AB＝CD，AD＝BC，∠ABC＝∠ADC，由等边三角形的性质可得BE＝EA＝AB＝CD＝CF＝DF，∠EBA＝∠CDF＝60°，由“SAS”可证△ADF≌△CBE，可得EC＝AF，由两组对边相等的四边形是平行四边形可证四边形AECF为平行四边形．
∵四边形ABCD是平行四边形
∴AB＝CD，AD＝BC，∠ABC＝∠ADC
∵△ABE和△CDF是等边三角形
∴BE＝EA＝AB＝CD＝CF＝DF，∠EBA＝∠CDF＝60°
∴∠ADF＝∠EBC，且AD＝BC，BE＝DF
∴△ADF≌△CBE（SAS）
∴EC＝AF，且AE＝CF
∴四边形AECF为平行四边形.
文敬图书课时先锋系列答案科目：初中数学 来源： 题型：
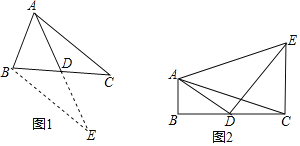
【题目】数学兴趣小组在活动时，老师提出了这样一个问题：如图1，在
中，
，
，D是BC的中点，求BC边上的中线AD的取值范围．
小明在组内经过合作交流，得到了如下的解决方法：延长AD到E，使
，请补充完整证明“
≌
”的推理过程．
求证：≌
证明：
延长AD到点E，使
在和中
已作
，
______，
中点定义，
≌
______，
探究得出AD的取值范围是______；
（感悟）解题时，条件中若出现“中点”“中线”等字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中．
（问题解决）
如图2，中，
，
，AD是的中线，
，
，且
，求AE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某中学开通了互联网家校合育教育平台，为了解家长使用平台的情况，学校将家长的使用情况分为“经常使用”、“偶尔使用”和‘不使用’三种类型，借助该平台大数据功能，汇总出该校吧（1）班和八（2）班全体家长的使用情况，并绘制成如图所示的两幅变质的统计图：
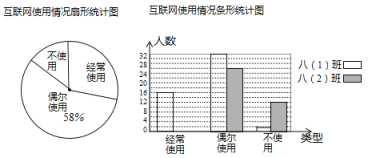
请根据图中信息解答下列问题
（1）此次调查的家长总人数是___________；
（2）扇形统计图中代表“不使用”类型的扇形圆心角的度数是___________度；算出八（2）班全体家长“经常使用”平台的人数并补全条形统计图；
（3）若该校八年级家长共有1200人，根据此次调查结果估计该校八年级中“经常使用”类型的家长月有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
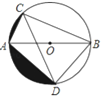
【题目】如图，AB为⊙O的直径，弦AC=2，∠ABC=30°，∠ACB的平分线交⊙O于点D，求：
（1）BC、AD的长；
（2）图中两阴影部分面积的和．
查看答案和解析>>
科目：初中数学 来源： 题型：
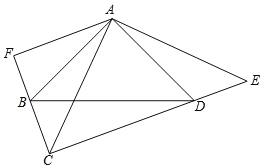
【题目】如图，∠BAD＝∠CAE＝90°，AB＝AD，AE＝AC，F是CB延长线上一点，AF⊥CF，垂足为F．下列结论：①∠ACF＝45°；②四边形ABCD的面积等于
AC2；③CE＝2AF；④S△BCD＝S△ABF+S△ADE；其中正确的是（ ）
A.①②B.②③C.①②③D.①②③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中，点E、F分别在BC、AB边上，且∠BEF+∠BFE﹣∠B＝∠A．
（1）如图1，求证：AB＝AC；
（2）如图2，延长EF交CA的延长线于D，点G是线段CE上一点，且∠CDE＝∠BDG＝90°，若∠BFE＝2∠DBA，求∠DGB的度数．
（3）如图3，在（2）的条件下，EG＝AC，CD＝8，求△BDG的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
