
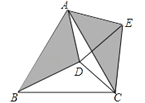
【题目】在△ABC中,点E、F分别在BC、AB边上,且∠BEF+∠BFE﹣∠B=∠A.

(1)如图1,求证:AB=AC;
(2)如图2,延长EF交CA的延长线于D,点G是线段CE上一点,且∠CDE=∠BDG=90°,若∠BFE=2∠DBA,求∠DGB的度数.
(3)如图3,在(2)的条件下,EG=AC,CD=8,求△BDG的面积.
【答案】(1)见解析;(2)45°;(3)16
【解析】
(1)由三角形内角和定理可得∠B=∠C,可证AB=AC;
(2)由余角的性质和三角形外角性质可得∠DBA=∠BDE=∠CDG,由直角三角形的性质可求解;
(3)如图3中,作DH⊥BC于H,GP∥AB交AC于P,GN⊥BC交AC于N,作AT⊥AB交BD的延长线于T,连接EN.利用全等三角形的性质想办法证明CN=2NG,推出∠C=30°即可解决问题.
解:(1)如图1中,
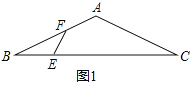
∵∠BEF+∠BFE﹣∠B=∠A,
∴∠BEF+∠BFE=∠A+∠B,
∵∠BEF+∠BFE+∠B=∠A+∠B+∠C=180°,
∴∠B=∠C,
∴AB=AC.
(2)如图2中,
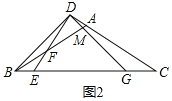
∵∠CDE=∠BDG=90°,
∴∠BDE=∠CDG,
∵∠BFE=2∠DBA=∠DBA+∠BDE,
∴∠DBA=∠BDE=∠CDG,
∵∠ABC=∠ACB,
∴∠ABC+∠DBA=∠ACB+∠CDG,
∴∠DBG=∠DGB,且∠BDG=90°,
∴∠DGB=∠DBG=45°.
(3)如图3中,作DH⊥BC于H,GP∥AB交AC于P,GN⊥BC交AC于N,作AT⊥AB交BD的延长线于T,连接EN.
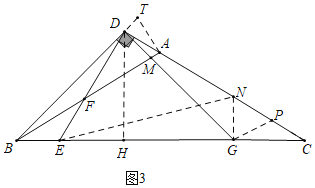
∵AB∥PG,
∴∠BAD=∠DPG,∠PGC=∠ABC,
∵AB=AC,
∴∠ABC=∠C=∠PGC,
∴PG=PC,
∵∠DBA=∠GDP,DB=DG,
∴△DBA≌△DGP(AAS),
∴AD=PG=PC,
∵∠PCG+∠CNG=90°,∠PGC+∠PGN=90°,
∴∠PNG=∠PGN,
∴PG=PN=PC,
∵∠EGN=∠EDN=90°,
∴D,E,G,N四点共圆,
∴∠NEG=∠GDN=∠ABT,
∵∠EGN=∠BAT=90°,AB=AC=EG,
∴△BAT≌△EGN(ASA),
∴AT=NG,
∵∠T+∠ABD=90°,∠ADT+∠BDF=90°,∠ABD=∠BDF,
∴∠T=∠ADT,
∴AD=AT=GN=PC=PN,
∴CN=2GN,
∴∠C=30°,
∵DH⊥BC,
∴∠DHC=90°,
∴DH=![]() CD=4,
CD=4,
∵△BGD是等腰直角三角形,DH⊥BG,
∴BH=HG,
∴BG=2DH=8,
∴S△BGD=![]() BGDH=
BGDH=![]() ×8×4=16.
×8×4=16.


科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | ﹣6 | 0 | 4 | 6 | 6 | … |
从上表可知,下列说法正确的有多少个
①抛物线与x轴的一个交点为(﹣2,0);
②抛物线与y轴的交点为(0,6);
③抛物线的对称轴是直线x=![]() ;
;
④抛物线与x轴的另一个交点为(3,0);
⑤在对称轴左侧,y随x增大而减少.
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一根长18cm的牙刷置于底面直径为5cm、高为12cm的圆柱形水杯中,牙刷露在杯子外面的长度为hcm,则h的取值范围是( )
A. 5cm<h≤6cm B. 6cm<h≤7cm C. 5cm≤h≤6cm D. 5cm≤h<6cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点D为CB延长线上一点,点E是AC的中点,连接DE交AB于点F,以DE为边向下作等边△DEG,连接CG、FG,若FG⊥DE,BD+BF=7,则CG的长为_____.
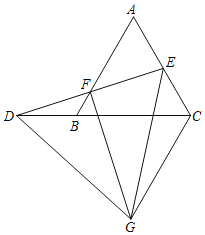
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,则∠CDE的正切值为 ( )
A. ![]() B. 2
B. 2![]() C. 3
C. 3![]() D. 4
D. 4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学准备围建一个矩形苗圃,其中一边靠墙,另外三边用长为![]() 米的篱笆围成,若墙长为
米的篱笆围成,若墙长为![]() 米,设这个苗圃垂直于墙的一边长为
米,设这个苗圃垂直于墙的一边长为![]() 米.
米.

![]() 若苗圃园的面积为
若苗圃园的面积为![]() 平方米,求
平方米,求![]() 的值;
的值;
![]() 若平行于墙的一边长不小于
若平行于墙的一边长不小于![]() 米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值,如果没有,请说明理由.
米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值,如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,把△ABC绕AB边上的点D顺时针旋转,旋转角为α(0°<α<180°),得到Rt△A′DE,A′C′交AB于点E,若AD=BE,则AD的长为_____

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com