
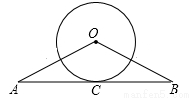
如图,在△ABO中,OA=OB,C是边AB的中点,以O为圆心的圆过点C.
(1)求证:AB与⊙O相切;
(2)若∠AOB=120°,AB=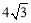 ,求⊙O的面积.
,求⊙O的面积.
科目:初中数学 来源:2014年初中毕业升学考试(广东汕尾卷)数学(解析版) 题型:解答题
如图,在Rt 中,
中, ,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.
,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.
(1)求证:点E是边BC的中点;
(2)求证: ;
;
(3)当以点O、D、E、C为顶点的四边形是正方形时,求证:△ABC是等腰直角三角形.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广东梅州卷)数学(解析版) 题型:解答题
如图,已知抛物线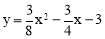 与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
(1)直接写出A、D、C三点的坐标;
(2)在抛物线的对称轴上找一点M,使得MD+MC的值最小,并求出点M的坐标;
(3)设点C关于抛物线对称的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广东梅州卷)数学(解析版) 题型:填空题
如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角. 当小球第1次碰到矩形的边时的点为P1,第2次碰到矩形的边时的点为P2,……第n次碰到矩形的边时的点为Pn. 则点P3的坐标是 ,点P2014的坐标是 .

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(安徽卷)数学(解析版) 题型:解答题
如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com