
如图,已知抛物线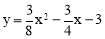 与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
(1)直接写出A、D、C三点的坐标;
(2)在抛物线的对称轴上找一点M,使得MD+MC的值最小,并求出点M的坐标;
(3)设点C关于抛物线对称的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,求出点P的坐标;若不存在,请说明理由.

(1)A(4,0) 、D(-2,0)、C(0,-3);(2)连接AC,则AC与抛物线的对称轴交点M即为所求,M (1, );(3)存在,(-2,0)或(6,6).
);(3)存在,(-2,0)或(6,6).
【解析】
试题分析:(1)在 中令
中令 ,解得
,解得 ,
,
∴A(4,0) 、D(-2,0).
在 中令
中令 ,得
,得 ,∴C(0,-3).
,∴C(0,-3).
(2)连接AC,根据轴对称的性质,AC与抛物线的对称轴交点M即为所求,从而应用待定系数法求出AC的解析式,再求出抛物线的对称轴,即可求得点M的坐标.
(3)分BC为梯形的底边和BC为梯形的腰两种情况讨论即可.
试题解析:(1)A(4,0) 、D(-2,0)、C(0,-3)
(2)如图,连接AC,则AC与抛物线的对称轴交点M即为所求.
设直线AC的解析式为 ,则
,则 ,解得
,解得 .
.
∴直线AC的解析式为 .
.
∵ 的对称轴是直线
的对称轴是直线 ,
,
把x=1代入 得
得
`∴M(1, ).
).

(3)存在,分两种情况:
①如图,当BC为梯形的底边时,点P与D重合时,四边形ADCB是梯形,此时点P为(-2,0).

②如图,当BC为梯形的腰时,过点C作CP//AB,与抛物线交于点P,
∵点C,B关于抛物线对称,∴B(2,-3)
设直线AB的解析式为 ,则
,则 ,解得
,解得 .
.
∴直线AB的解析式为 .
.
∵CP//AB,∴可设直线CP的解析式为 .
.
∵点C在直线CP上,∴ .
.
∴直线CP的解析式为 .
.
联立 ,解得
,解得 ,
,
∴P(6,6).

综上所述,在抛物线上存在点P,使得以A、B、C、P四点为顶点的四边形为梯形,点P的坐标为(-2,0)或(6,6).
考点:1.二次函数综合题;2.待定系数法的应用;3.曲线上点的坐标与方程的关系;4. 轴对称的应用(最短线路问题);5.二次函数的性质;6.梯形存在性问题;7.分类思想的应用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014年初中毕业升学考试(广西北海卷)数学(解析版) 题型:选择题
若两圆的半径分别是1cm和4cm,圆心距为5cm,则这两圆的位置关系是( )
A.内切 B.相交 C.外切 D.外离
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广东梅州卷)数学(解析版) 题型:解答题
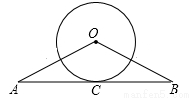
如图,在△ABO中,OA=OB,C是边AB的中点,以O为圆心的圆过点C.
(1)求证:AB与⊙O相切;
(2)若∠AOB=120°,AB=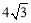 ,求⊙O的面积.
,求⊙O的面积.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广东梅州卷)数学(解析版) 题型:填空题
如图,把△ABC绕点C按顺时针方向旋转35°,得到△A’B’C,A’B’交AC于点D,若∠A’DC=90°,则∠A= °.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(安徽卷)数学(解析版) 题型:解答题
如图1,正六边形ABCDEF的边长为a,P是BC边上一动点,过P作PM∥AB交AF于M,作PN∥CD交DE于N.
(1)①∠MPN= ;
②求证:PM+PN=3a;
(2)如图2,点O是AD的中点,连接OM、ON,求证:OM=ON;
(3)如图3,点O是AD的中点,OG平分∠MON,判断四边形OMGN是否为特殊四边形?并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com