
如图1,正六边形ABCDEF的边长为a,P是BC边上一动点,过P作PM∥AB交AF于M,作PN∥CD交DE于N.
(1)①∠MPN= ;
②求证:PM+PN=3a;
(2)如图2,点O是AD的中点,连接OM、ON,求证:OM=ON;
(3)如图3,点O是AD的中点,OG平分∠MON,判断四边形OMGN是否为特殊四边形?并说明理由.

(1)①60°,②证明见解析;
(2)证明见解析;
(3)四边形MONG是菱形,理由见解析.
【解析】
试题分析:(1)①运用∠MPN=180°-∠BPM-∠NPC求解,②作AG⊥MP交MP于点G,BH⊥MP于点H,CL⊥PN于点L,DK⊥PN于点K,利用MP+PN=MG+GH+HP+PL+LK+KN求解,
(2)连接OE,由△OMA≌△ONE证明,
(3)连接OE,由△OMA≌△ONE,再证出△GOE≌△NOD,由△ONG是等边三角形和△MOG是等边三角形求出四边形MONG是菱形.
试题解析:(1)①∵四边形ABCDEF是正六边形,
∴∠A=∠B=∠C=∠D=∠E=∠F=120°.
又∴PM∥AB,PN∥CD,
∴∠BPM=60°,∠NPC=60°,
∴∠MPN=180°-∠BPM-∠NPC=180°-60°-60°=60°,
故答案为;60°.
②如图1,作AG⊥MP交MP于点G,BH⊥MP于点H,CL⊥PN于点L,DK⊥PN于点K,
MP+PN=MG+GH+HP+PL+LK+KN.
∵正六边形ABCDEF中,PM∥AB,作PN∥CD,
∵∠AMG=∠BPH=∠CPL=∠DNK=60°,
∴ ,
,
∵AM=BP,PC=DN,
∴MG+HP+PL+KN=a,GH=LK=a,
∴MP+PN=MG+GH+HP+PL+LK+KN=3a.
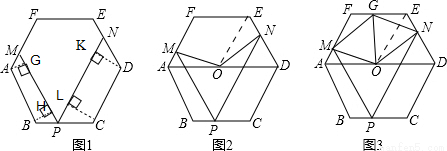
(2)如图2,连接OE,
∵四边形ABCDEF是正六边形,AB∥MP,PN∥DC,
∴AM=BP=EN,
又∵∠MAO=∠NOE=60°,OA=OE,
在△ONE和△OMA中,
 ,
,
∴△OMA≌△ONE(SAS),
∴OM=ON.
(3)如图3,连接OE,
由(2)得,△OMA≌△ONE,
∴∠MOA=∠EON,
∵EF∥AO,AF∥OE,
∴四边形AOEF是平行四边形,
∴∠AFE=∠AOE=120°,
∴∠MON=120°,
∴∠GON=60°,
∵∠GON=60°-∠EON,∠DON=60°-∠EON,
∴∠GOE=∠DON,
∵OD=OE,∠ODN=∠OEG,
在△GOE和∠DON中,
 ,
,
∴△GOE≌△NOD(ASA),
∴ON=OG,
又∵∠GON=60°,
∴△ONG是等边三角形,
∴ON=NG,
又∵OM=ON,∠MOG=60°,
∴△MOG是等边三角形,
∴MG=GO=MO,
∴MO=ON=NG=MG,
∴四边形MONG是菱形.
考点:四边形综合题.


 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源:2014年初中毕业升学考试(广东梅州卷)数学(解析版) 题型:解答题
如图,已知抛物线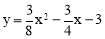 与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
(1)直接写出A、D、C三点的坐标;
(2)在抛物线的对称轴上找一点M,使得MD+MC的值最小,并求出点M的坐标;
(3)设点C关于抛物线对称的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(山东滨州卷)数学(解析版) 题型:选择题
下列四组线段中,可以构成直角三角形的是( )
A.4,5,6 B.1.5,2,2.5 C.2,3,4 D.1, , 3
, 3
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(山东济宁卷)数学(解析版) 题型:选择题
如果圆锥的母线长为5cm,底面半径为2cm,那么这个圆锥的侧面积是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(安徽卷)数学(解析版) 题型:解答题
如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号).

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(安徽卷)数学(解析版) 题型:填空题
据报载,2014年我国将发展固定宽带接入新用户25000000户,其中25000000用科学记数法表示
为 .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川雅安卷)数学(解析版) 题型:计算题
(1)|﹣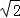 |+(﹣1)2014﹣2cos45°+
|+(﹣1)2014﹣2cos45°+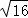 .
.
(2)先化简,再求值: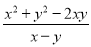 ÷(
÷(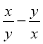 ),其中x=
),其中x=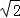 +1,y=
+1,y=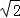 ﹣1.
﹣1.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川达州卷)数学(解析版) 题型:选择题
2014年5月21日,中国石油天然气集团公司与俄罗斯天然气工业股份公司在上海签署了《中俄东线供气购销合同》,这份有效期为30年的合同规定,从2018年开始供气,每年的天然气供应量为380亿立方米,380亿立方米用科学记数法表示为( )
A.3.8×1010m3 B.38×109m3 C.380×108m3 D.3.8×1011m3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com