
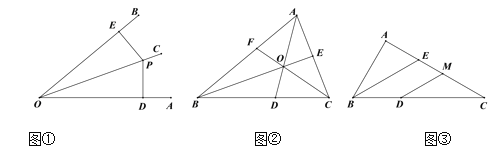
【题目】教材呈现:如图是华师版八年级上册数学教材第96页的部分内容.

(1)定理证明:请根据教材中的分析,结合图①,写出“角平分线的性质定理”完整的证明过程.
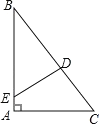
(2)定理应用:如图②,在△ABC中,AD、BE分别是∠BAC、∠ABC的角平分线,AD、BE的交点为O,连结CO交AB于点F,求证:∠ACF=∠BCF.
(3)如图③,在(2)的条件下,若BE=CE,∠C=30°,△ABD沿AD翻折使点B落在边AC上的点M处,连结DM,其中AB=![]() ,则S△DCM= .
,则S△DCM= .
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)利用AAS可证△PEO≌PDO,可得PD=PE;
(2)由角平分线的性质可得,OG=OH,OH=OI,可得OG=OI,由在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上,可得结论;
(3)由角平分线的性质和等腰三角形的性质可求∠BAC=90°,可求AE,BE,CE,BC的长,即可求BD=DM=CM的长,由三角形面积公式可求解.
证明:(1)∵OC平分∠AOB,
∴∠BOC=∠AOC,
∵PD⊥OA,PE⊥OB,
∴∠PEO=∠PDO=90°,且∠BOC=∠AOC,OP=OP,
∴△PEO≌PDO(AAS)
∴PD=PE;
(2)如图,作OG⊥BC于G,OH⊥AB于H,OI⊥AC于I.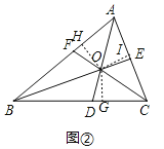
由(1)得,OG=OH,OH=OI.
∴OG=OI,且OG⊥BC,OI⊥AC,
∴点O在∠ACB的平分线上,
∴∠ACF=∠BCF.
(3)如图,连接AD,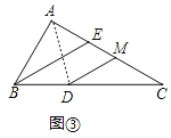
∵BE=CE,
∴∠C=∠EBC=30°,
∵AD、BE分别是∠BAC、∠ABC的角平分线,
∴∠ABE=∠CBE=30°,∠BAD=∠CAD.
∴∠BAC=90°,且AB=![]() ,
,
∴AE=1,BE=2=CE,
∴AC=3,BC=![]() .
.
∵△ABD沿AD翻折使点B落在边AC上的点M处,
∴AB=AM=![]() ,BD=DM,∠AMD=∠ABC=60°
,BD=DM,∠AMD=∠ABC=60°
∴CM=AC-AM=![]() ,
,
∵∠MDC+∠MCD=∠AMD=60°,
∴∠MDC=∠MCD=30°,
∴MC=DM=BD=![]() ,CD=BC-BD=
,CD=BC-BD=![]() ,
,
∴S△DMC=![]() =
=![]() .
.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() (a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0).则下面的四个结论:①2a+b=0;②4a-2b+c<0;③ac>0;④当y<0时,x<-1或x>2.其中正确的个数是
(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0).则下面的四个结论:①2a+b=0;②4a-2b+c<0;③ac>0;④当y<0时,x<-1或x>2.其中正确的个数是
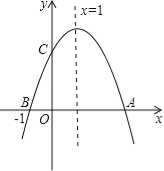
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PB:PC=1:2.

(1)求证:AC平分∠BAD;
(2)探究线段PB,AB之间的数量关系,并说明理由;
(3)若AD=3,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在某次斯诺克比赛中,白球位于点 A 处,在点 A 正北方向的点 B 处有一颗红球,在点 A 正东方向 C 处有一颗黑球,在 BC 正中间的点 D 处有一颗篮球,其中点 C 在点 B 的南偏东 37°方向上,选手将白球沿正北方想推进 10cm 到达点 E 处时,测得点D 在点E 的北偏东45°方向上,求此时白球与红球的距离有多远?(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈ ![]() ,tan37°≈
,tan37°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
港珠澳大桥是世界上最长的跨海大桥,是被誉为“现代世界七大奇迹”的超级工程,它是我国从桥梁大国走向桥梁强国的里程碑之作.开通后从香港到珠海的车程由原来的180千米缩短到50千米,港珠澳大桥的设计时速比按原来路程行驶的平均时速多40千米,若开通后按设计时速行驶,行驶完全程时间仅为原来路程行驶完全程时间的![]() ,求港珠澳大桥的设计时速是多少.
,求港珠澳大桥的设计时速是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
(1)将△ABC向下平移5个单位后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,请画出△A2B2C2;
(3)判断以O,A1,B为顶点的三角形的形状.(无须说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
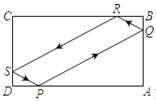
【题目】如图![]() 是一个矩形桌子,一小球从
是一个矩形桌子,一小球从![]() 撞击到
撞击到![]() ,反射到
,反射到![]() ,又从
,又从![]() 反射到
反射到![]() ,从
,从![]() 反射回原处
反射回原处![]() ,入射角与反射角相等(例如
,入射角与反射角相等(例如![]() 等),已知
等),已知![]() ,
,![]() ,
,![]() .则小球所走的路径的长为__________.
.则小球所走的路径的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,BC=8cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).
(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;
(2)①当t为 时,以A、F、C、E为顶点的四边形是平行四边形(直接写出结果);
②当t为 时,四边形ACFE是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
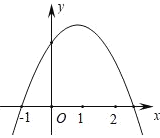
【题目】如图,已知抛物线y=ax2+bx+c经过点(﹣1,0),以下结论:①2a+b>0;②a+c<0;③4a+2b+c>0;④b2﹣5a2>2ac.其中正确的是( )
A. ①②B. ③④C. ②③④D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com