
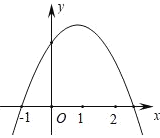
【题目】如图,已知抛物线y=ax2+bx+c经过点(﹣1,0),以下结论:①2a+b>0;②a+c<0;③4a+2b+c>0;④b2﹣5a2>2ac.其中正确的是( )
A. ①②B. ③④C. ②③④D. ①②③④
【答案】B
【解析】
利用对称轴的位置则可对①进行判断;由a﹣b+c=0,即a+c=b>0,可对②进行判断;由x=2时,y>0,可对③进行判断;把(﹣1,0)代入解析式得a﹣b+c=0,可得出2a+c>0,再由a<0,可知c>0则c﹣2a>0,故可得出(c+2a)(c﹣2a)>0,即b2﹣2ac﹣5a2>0,可对④进行判断.
解:由图象可知a<0,0<﹣![]() <1,
<1,
∴b<﹣2a,
∴2a+b<0,所以①错误;
∵﹣![]() >0,a<0,
>0,a<0,
∴b>0,
当x=﹣1时,y1=a﹣b+c=0,
∴a+c=b>0,所以②错误;
∵当x=2时,y>0,
∴4a+2b+c>0﹣﹣﹣﹣②,所以③正确;
∵过(﹣1,0),代入得a﹣b+c=0,
∴b2﹣2ac﹣5a2=(a+c)2﹣2ac﹣5a2=c2﹣4a2=(c+2a)(c﹣2a)
又∵4a+2b+c>0
4a+2(a+c)+c>0
即2a+c>0①
∵a<0,
∴c>0
则c﹣2a>0②
由①②知(c+2a)(c﹣2a)>0,
所以b2﹣2ac﹣5a2>0,
即b2﹣5a2>2ac,所以④正确.
故选:B.


科目:初中数学 来源: 题型:
【题目】已知直线l:y=kx+1与抛物线y=x2-4x
(1)求证:直线l与该抛物线总有两个交点;
(2)设直线l与该抛物线两交点为A,B,O为原点,当k=-2时,求△OAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为改善办学条件,计划采购A、B两种型号的空调,已知采购3台A型空调和2台B型空调,需费用39000元;4台A型空调比5台B型空调的费用多6000元.
(1)求A型空调和B型空调每台各需多少元;
(2)若学校计划采购A、B两种型号空调共30台,且A型空调的台数不少于B型空调的一半,两种型号空调的采购总费用不超过217000元,该校共有哪几种采购方案?
(3)在(2)的条件下,采用哪一种采购方案可使总费用最低,最低费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
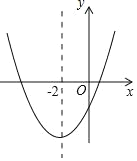
【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,顶点坐标为(﹣2,﹣9a),下列结论:①abc>0;②4a+2b+c>0;③5a﹣b+c=0;④若方程a(x+5)(x﹣1)=﹣1有两个根x1和x2,且x1<x2,则﹣5<x1<x2<1;⑤若方程|ax2+bx+c|=2有四个根,则这四个根的和为﹣4.其中正确的结论有( )
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC、BD相交于点O,△ABE与△ABO关于AB轴对称.
(1)求证:四边形AEBO是菱形;
(2)若AB=6,∠AOB=60°,求四边形AEBO的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
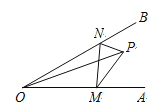
【题目】如图,∠AOB![]() 30°,点P是∠AOB内的一定点,且OP
30°,点P是∠AOB内的一定点,且OP![]() 6,若点M,N分别是射线OA,OB上异于点O的动点,则△PMN周长的最小值是__________.
6,若点M,N分别是射线OA,OB上异于点O的动点,则△PMN周长的最小值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
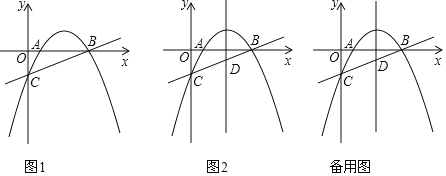
【题目】如图,直线![]() 与x轴、y轴分别交于BC两点,抛物线
与x轴、y轴分别交于BC两点,抛物线![]() 经过B、C两点,且与x轴交于点A
经过B、C两点,且与x轴交于点A
(1)求该抛物线的函数表达式;
(2)已知点M是第一象限内抛物线上的一个动点,过点M作MN平行于y轴交直线BC于点N,连接AM、BM、AN,求四边形MANB面积S的最大值,并求出此时点M的坐标;
(3)抛物线的对称轴交直线BC于点D,若Q为y轴上一点,则在抛物线上是否存在一点P,使得以B、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,与直线
,与直线![]() 交于点
交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求该抛物线的解析式.
(2)点![]() 是抛物线上第四象限上的一个动点,连接
是抛物线上第四象限上的一个动点,连接![]() ,
,![]() ,当
,当![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标.
的坐标.
(3)将抛物线的对称轴向左平移3个长度单位得到直线![]() ,点
,点![]() 是直线
是直线![]() 上一点,连接
上一点,连接![]() ,
,![]() ,若直线
,若直线![]() 上存在使
上存在使![]() 最大的点
最大的点![]() ,请直接写出满足条件的点
,请直接写出满足条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com