
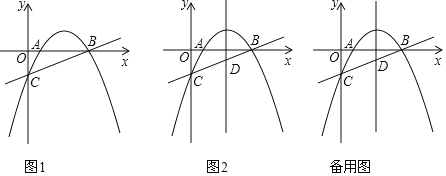
【题目】如图,直线![]() 与x轴、y轴分别交于BC两点,抛物线
与x轴、y轴分别交于BC两点,抛物线![]() 经过B、C两点,且与x轴交于点A
经过B、C两点,且与x轴交于点A
(1)求该抛物线的函数表达式;
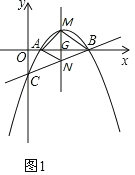
(2)已知点M是第一象限内抛物线上的一个动点,过点M作MN平行于y轴交直线BC于点N,连接AM、BM、AN,求四边形MANB面积S的最大值,并求出此时点M的坐标;
(3)抛物线的对称轴交直线BC于点D,若Q为y轴上一点,则在抛物线上是否存在一点P,使得以B、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)当t=
;(2)当t=![]() 时,S四边形MANB的最大值=5,此时点M
时,S四边形MANB的最大值=5,此时点M![]() ;(3)P坐标为
;(3)P坐标为![]() 或
或![]() 或
或![]() .
.
【解析】
(1)直线![]() 与x轴、y轴的交点为B(5,0),C(0,﹣2),代入抛物线解析式可求出a,c的值;
与x轴、y轴的交点为B(5,0),C(0,﹣2),代入抛物线解析式可求出a,c的值;
(2)设点![]() ,用含t的代数式表示四边形MANB的面积,得到S与t的函数关系式,利用二次函数最大值求出t的值;
,用含t的代数式表示四边形MANB的面积,得到S与t的函数关系式,利用二次函数最大值求出t的值;
(3)存在,分BD为平行四边形的边或对角线进行分类讨论.
解:(1)由![]() x﹣2=0得x=5,
x﹣2=0得x=5,
∴B(5,0),令x=0,得y=﹣2,
∴C(0,﹣2),
由题意得:![]() ,
,
解得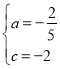 ,
,
∴抛物线解析式为 ![]() .
.
(2)如图1,设![]() ,
,
![]()
S四边形MANB=S△AMN+S△BMN
=![]() AGMN+
AGMN+![]() BGMN
BGMN
=![]() MN(AG+BG)
MN(AG+BG)
=![]() MNAB
MNAB
=![]() ×4(
×4(![]() t2+2t)
t2+2t)
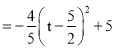
∵![]() <0,
<0,
∴当t=![]() 时,S四边形MANB的最大值=5,此时点M
时,S四边形MANB的最大值=5,此时点M![]() .
.
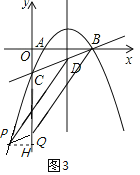
(3)存在.由为 ![]() ,
,
∴抛物线对称轴x=3.对称轴交x轴于F,
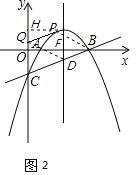
①以BD为边,PQ在BC上方,如图2,D(3,![]() ),F(3,0),
),F(3,0),
∵四边形BDQP是平行四边形,∴BD∥PQ,BD=PQ,
过点P作PH⊥y轴于H,
∴∠PHQ=∠BFD=90°,∠PQH=∠BCO=∠BDF,
∴△PQH≌△BDF,
∴PH=BF=2,HQ=FD=![]() ,
,
∴P(2,![]() ).
).
②以BD为边,PQ在BC下方,如图3,仿照①可求得P![]() ,
,
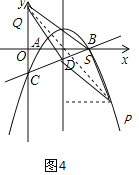
③以BD为平行四边形对角线,如图4,设BD中点为S,则S![]() ,
,
∵BPDQ是平行四边形,
∴BD与PQ互相平分,
∴SQ=SP,
∴S是PQ中点,
设![]() ,
,
∴![]() ,
,
∴a=8,
∴P(8,![]() )
)
综上所述,P坐标为![]() 或
或![]() 或
或![]() .
.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
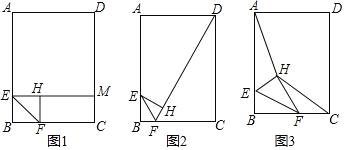
【题目】如图,点E,F分别在矩形ABCD的边AB,BC上,连接EF,将△BEF沿直线EF翻折得到△HEF,AB=8,BC=6,AE:EB=3:1.
(1)如图1,当∠BEF=45°时,EH的延长线交DC于点M,求HM的长;
(2)如图2,当FH的延长线经过点D时,求tan∠FEH的值;
(3)如图3,连接AH,HC,当点F在线段BC上运动时,试探究四边形AHCD的面积是否存在最小值?若存在,求出四边形AHCD的面积的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c经过点(﹣1,0),以下结论:①2a+b>0;②a+c<0;③4a+2b+c>0;④b2﹣5a2>2ac.其中正确的是( )
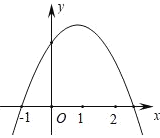
A. ①②B. ③④C. ②③④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小方与小辉在玩军棋游戏,他们定义了一种新的规则,用军棋中的“工兵”、“连长”、“地雷”比较大小,共有6个棋子,分别为1个“工兵”,2个“连长”,3个“地雷”游戏规则如下:①游戏时,将棋反面朝上,两人随机各摸一个棋子进行比赛,先摸者摸出的棋不放回;②“工兵”胜“地雷”,“地雷”胜“连长”,“连长”胜“工兵”;③相同棋子不分胜负.
(1)若小方先摸,则小方摸到“排长”的事件是 ;若小方先摸到了“连长”,小辉在剩余的5个棋子中随机摸一个,则这一轮中小方胜小辉的概率为 .
(2)如果先拿走一个“连长”,在剩余的5个棋子中小方先摸一个棋子,然后小辉在剩余的4个棋子中随机摸一个,求这一轮中小方获胜的概率 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=x+1的图象l与y轴交于点C,A1的坐标为(1,0),点B1在直线l上,且A1B1平行于y轴,连接CA1、OB1交于点P1,过点A1作A1B2∥OB1交直线l于点B2,过点B1作B1A2∥CA1交x轴于点A2,A1B2与B1A2交于点P2,……,按此进行下去,则点P2019的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某教学活动小组选定测量小山上方某信号塔PQ的高度,他们在A处测得信号塔顶端P的仰角为45°,信号塔低端Q的仰角为31°,沿水平地面向前走100米到处,测得信号塔顶端P的仰角为68°.求信号塔PQ的高度.(结果精确到0.1米.参考数据:sin68°≈ 0.93,cos68° ≈ 0.37,tan68° ≈ 2.48,tan31° ≈ 0.60,sin31° ≈ 0.52,cos31°≈0.86)
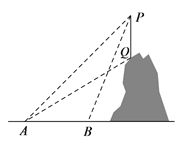
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,已知点A(﹣3,0),B(0,4),对△OAB连续作旋转变换,依次得到△1,△2,△3,△4,…,则△2019的直角顶点的坐标为( )
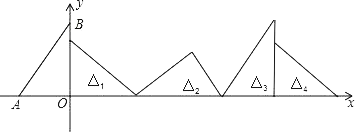
A. (8076,0)B. (8064,0)C. (8076,![]() )D. (8064,
)D. (8064,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了多少名购买者?
(2)请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为 度.
(3)若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于![]() MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.
MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com