
【题目】小方与小辉在玩军棋游戏,他们定义了一种新的规则,用军棋中的“工兵”、“连长”、“地雷”比较大小,共有6个棋子,分别为1个“工兵”,2个“连长”,3个“地雷”游戏规则如下:①游戏时,将棋反面朝上,两人随机各摸一个棋子进行比赛,先摸者摸出的棋不放回;②“工兵”胜“地雷”,“地雷”胜“连长”,“连长”胜“工兵”;③相同棋子不分胜负.
(1)若小方先摸,则小方摸到“排长”的事件是 ;若小方先摸到了“连长”,小辉在剩余的5个棋子中随机摸一个,则这一轮中小方胜小辉的概率为 .
(2)如果先拿走一个“连长”,在剩余的5个棋子中小方先摸一个棋子,然后小辉在剩余的4个棋子中随机摸一个,求这一轮中小方获胜的概率 .

科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
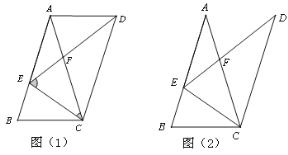
【题目】在△ABC中,AB=AC,BC=2,将△ABC绕点C顺针方向旋转α(0°<α<360°),得到△DEC,使点E在AB边上。
(1)如图1,连接AD,
①求证:四边形ABCD是平行四边形;
② 当AE=AD时,求旋转角α的度数;
(2)如图2,若AE=2BE,求AB的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
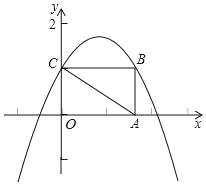
【题目】如图,平面直角坐标系xOy中,矩形OABC的顶点A,C分别在x轴,y轴的正半轴上,且点C的坐标是(0,1),点B的坐标是(![]() ,1),抛物线y=﹣x2+bx+c经过点B和点C.
,1),抛物线y=﹣x2+bx+c经过点B和点C.
(1)求抛物线y=﹣x2+bx+c的表达式:
(2)将△OAC沿直线AC折叠,点O的对称点记为点D,请判断:点D是否在抛物线上?并说明理由;
(3)点E为线段AC上的一个动点.
①若点P在抛物线上,其横坐标为m,当PE⊥AC且PE=![]() 时.请直接写出m的值;
时.请直接写出m的值;
②若点F为线段AB上一个动点,且CE=AF,当OE+OF的值最小时,请直接写出点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A的坐标是(4,0),并且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.
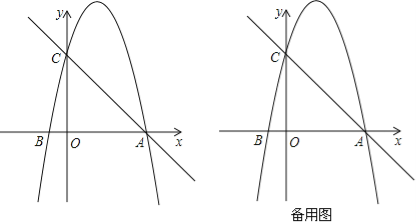
(1)求抛物线的解析式;
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,点D为BC边上一点(不与点B,点C重合),连结AD,点E、点F分别为AB、AC上的点,且EF∥BC,交AD于点G,连结BG,并延长BG交AC于点H.已知![]() =2,①若AD为BC边上的中线,
=2,①若AD为BC边上的中线,![]() 的值为
的值为![]() ;②若BH⊥AC,当BC>2CD时,
;②若BH⊥AC,当BC>2CD时,![]() <2sin∠DAC.则( )
<2sin∠DAC.则( )
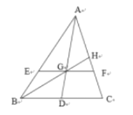
A. ①正确;②不正确B. ①正确;②正确
C. ①不正确;②正确D. ①不正确;②正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,2AB>BC,点E和点F为边AD上两点,将矩形沿着BE和CF折叠,点A和点D恰好重合于矩形内部的点G处,
(1)当AB=BC时,求∠GEF的度数;
(2)若AB=![]() ,BC=2,求EF的长.
,BC=2,求EF的长.
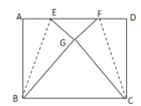
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校“两会”知识竞赛培训活动中,在相同条件下对甲、乙两名学生进行了10次测验.
①收集数据:分别记录甲、乙两名学生10次测验成绩(单位:分)
次数 成绩 学生 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
甲 | 74 | 84 | 89 | 83 | 86 | 81 | 86 | 84 | 86 | 86 |
乙 | 82 | 73 | 81 | 76 | 81 | 87 | 81 | 90 | 92 | 96 |
②整理数据:两组数据的平均数、中位数、众数、方差如下表所示:
统计量 学生 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 83.9 | ______ | 86 | 15.05 |
乙 | 83.9 | 81.5 | ______ | 46.92 |
③分析数据:根据甲、乙两名学生10次测验成绩绘制折线统计图:
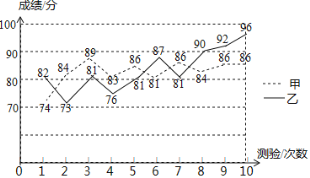
④得出结论:结合上述统计全过程,回答下列问题:
(1)补全②中的表格.
(2)判断甲、乙两名学生中, (填甲或乙)的成绩比较稳定,说明判断依据: .
(3)如果你是决策者,从甲、乙两名学生中选择一人代表学校参加知识竞赛,你会选择______(填“甲”或“乙),理由是:____ __.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,直线![]() ,点
,点![]() ,点
,点![]() ,动点
,动点![]() 在直线
在直线![]() 上,动点
上,动点![]() 、
、![]() 在
在![]() 轴正半轴上,连接
轴正半轴上,连接![]() 、
、![]() 、
、![]() .
.
(1)若点![]() ,求直线
,求直线![]() 的解析式;
的解析式;
(2)如图![]() ,当
,当![]() 周长最小时,连接
周长最小时,连接![]() ,求
,求![]() 的最小值,并求出此时点
的最小值,并求出此时点![]() 的坐标;
的坐标;
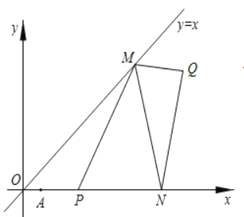
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com