
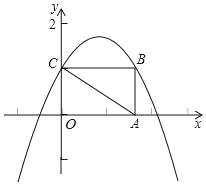
【题目】如图,平面直角坐标系xOy中,矩形OABC的顶点A,C分别在x轴,y轴的正半轴上,且点C的坐标是(0,1),点B的坐标是(![]() ,1),抛物线y=﹣x2+bx+c经过点B和点C.
,1),抛物线y=﹣x2+bx+c经过点B和点C.
(1)求抛物线y=﹣x2+bx+c的表达式:
(2)将△OAC沿直线AC折叠,点O的对称点记为点D,请判断:点D是否在抛物线上?并说明理由;
(3)点E为线段AC上的一个动点.
①若点P在抛物线上,其横坐标为m,当PE⊥AC且PE=![]() 时.请直接写出m的值;
时.请直接写出m的值;
②若点F为线段AB上一个动点,且CE=AF,当OE+OF的值最小时,请直接写出点F的坐标.
【答案】(1)y=﹣x2+![]() x+l;(2)不在;(3)①m=2
x+l;(2)不在;(3)①m=2![]() ±2
±2![]() 或
或![]() ;②
;②![]()
【解析】
(1)将点B、C坐标代入二次函数表达式,即可求解;
(2)不在,理由:利用△CDG∽△DHA,求得点D的坐标是(![]() ,
,![]() ),即可求解;
),即可求解;
(3)①设点P的坐标为(m,﹣m2+![]() m+1),点E(n,﹣
m+1),点E(n,﹣![]() n+1),利用EH=|﹣
n+1),利用EH=|﹣![]() n+1+m2﹣
n+1+m2﹣![]() m﹣1|=1,PH=|m﹣n|=
m﹣1|=1,PH=|m﹣n|=![]() ,即可求解;
,即可求解;
②将矩形ABCO围绕点C逆时针旋转60°至矩形O′A′B′C,则图示位置为图象旋转后的位置,当B′、E、O三点共线时,OE+OF=OB′最小,即可求解.
解:(1)将点B坐标代入二次函数表达式得:1=﹣3+![]() b+1,解得:b=
b+1,解得:b=![]() ,
,
故二次函数表达式为:y=﹣x2+![]() x+l;
x+l;
(2)不在,理由:
过点D作x轴的平行线分别交AB的延长线和y轴于点G、H,

∴∠CDA=90°,∠GDC+HDA∠=90°,∠HDA+∠DAH=90°,
∴∠DAH=∠GDC,
∴△CDG∽△DHA,
∴![]() ,
,
解得:DG=![]() ,HA=
,HA=![]() ,故:点D的坐标是(
,故:点D的坐标是(![]() ,
,![]() ),
),
将![]() 代入抛物线表达式,则y=
代入抛物线表达式,则y=![]() ≠
≠![]() 所以点D不在抛物线上;
所以点D不在抛物线上;
(3)①∵PE⊥AC,∴∠PEH+∠HEA=90°,∠HEA+∠EAO=90°,

∴∠PEH=∠CAO=α,
点B的坐标是(![]() ,1),tan∠ABC=
,1),tan∠ABC=![]() =tanα,即:∠ABC=30°=α,
=tanα,即:∠ABC=30°=α,
PH=PEsinα=![]() ,EH=1,
,EH=1,
把点AC的表达式为:y=kx+1,把点A坐标代入并求解得:
直线AC的表达式为:y=﹣![]() x+1,
x+1,
设点P的坐标为(m,﹣m2+![]() m+1),点E(n,﹣
m+1),点E(n,﹣![]() n+1),
n+1),
EH=|﹣![]() n+1+m2﹣
n+1+m2﹣![]() m﹣1|=1…①,
m﹣1|=1…①,
PH=|m﹣n|=![]() …②,
…②,
联立①②并解得:m=2![]() ±2
±2![]() 或
或![]() ;
;
②∵∠ABC=30°,∴△O′OC为等边三角形,
将矩形ABCO围绕点C逆时针旋转60°至矩形O′A′B′C,则图示位置为图象旋转后的位置,

连接O′F′、B′E、OE,∵CE=AF=A′F′,
∴四边形O′F′B′E为平行四边形,
∴OE+OF=OE+B′E,故:当B′、E、O三点共线时,OE+OF=OB′最小,
旋转后点B′O′与x轴垂直,则yB′=![]() AB+A′C=
AB+A′C=![]() +
+![]() =
=![]() ,同理xB′=
,同理xB′=![]() ,
,
即点B′(![]() ,
,![]() ),
),
则直线OB′的表达式为:y=![]() x,
x,
同理可得直线AC的表达式为:y=﹣![]() x+1,
x+1,
以上两式联立并求解得:x=![]() ,y=
,y=![]() ,
,
即点E(![]() ,
,![]() ),
),
同理可得点![]() .
.


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “任意画一个三角形,其内角和为![]() ”是随机事件;
”是随机事件;
B. 某种彩票的中奖率是![]() ,说明每买100张彩票,一定有1张中奖;
,说明每买100张彩票,一定有1张中奖;
C. “篮球队员在罚球线上投篮一次,投中”为随机事件;
D. 投掷一枚质地均匀的硬币100次,正面向上的次数一定是50次.
查看答案和解析>>
科目:初中数学 来源: 题型:
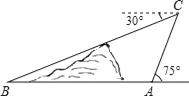
【题目】如图,在小山的东侧A点有一个热气球,由于受风的影响,以30米/分的速度沿与地面成75°角的方向飞行,25分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,则小山东西两侧A,B两点间的距离为( )米.
A. 750![]() B. 375
B. 375![]() C. 375
C. 375![]() D. 750
D. 750![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道不等式的两边加(或减)同一个数(或式子),不等号的方向不变.不等式组是否也具有类似的性质呢?请解答下列问题.
(1)完成下列填空:
已知 | 用“<”或“>”填空 |
| 5+2_____3+1 |
| ﹣3﹣1_____﹣5﹣2 |
| 1﹣2_____4+1 |
(2)一般地,如果![]() 那么a+c_____b+d(用“<”或“>”填空).请你说明上述性质的正确性.
那么a+c_____b+d(用“<”或“>”填空).请你说明上述性质的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前节能灯在城市已基本普及,今年山东省面向县级及农村地区推广节能灯,为响应号召,某商场计划购进甲、乙两种节能灯共1200只,这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲 | 25 | 30 |
乙 | 45 | 60 |
(1)如何进货,进货款恰好为46000元?
(2)如何进货,商场销售完节能灯时获利最多且不超过进货价的30%,此时利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小方与小辉在玩军棋游戏,他们定义了一种新的规则,用军棋中的“工兵”、“连长”、“地雷”比较大小,共有6个棋子,分别为1个“工兵”,2个“连长”,3个“地雷”游戏规则如下:①游戏时,将棋反面朝上,两人随机各摸一个棋子进行比赛,先摸者摸出的棋不放回;②“工兵”胜“地雷”,“地雷”胜“连长”,“连长”胜“工兵”;③相同棋子不分胜负.
(1)若小方先摸,则小方摸到“排长”的事件是 ;若小方先摸到了“连长”,小辉在剩余的5个棋子中随机摸一个,则这一轮中小方胜小辉的概率为 .
(2)如果先拿走一个“连长”,在剩余的5个棋子中小方先摸一个棋子,然后小辉在剩余的4个棋子中随机摸一个,求这一轮中小方获胜的概率 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,△ABC各顶点的坐标分别是A(﹣2,﹣4),B(0,﹣4),C(1,﹣1).
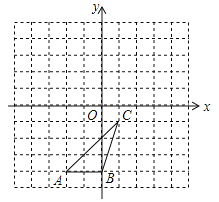
(1)在图中画出△ABC向左平移3个单位后的△A1B1C1;
(2)在图中画出△ABC绕原点O逆时针旋转90°后的△A2B2C2;
(3)在(2)的条件下,AC边扫过的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
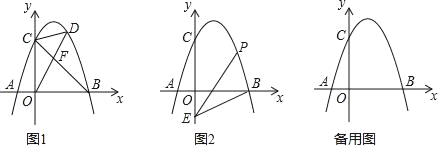
【题目】如图,抛物线y=ax2+2x+c(a<0)与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,OB=OC=3.
(1)求该抛物线的函数解析式.
(2)如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD,CD.OD交BC于点F,当S△COF:S△CDF=3:2时,求点D的坐标.
(3)如图2,点E的坐标为(0,![]() ),点P是抛物线上的点,连接EB,PB,PE形成的△PBE中,是否存在点P,使∠PBE或∠PEB等于2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
),点P是抛物线上的点,连接EB,PB,PE形成的△PBE中,是否存在点P,使∠PBE或∠PEB等于2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com