
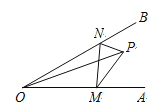
【题目】如图,∠AOB![]() 30°,点P是∠AOB内的一定点,且OP
30°,点P是∠AOB内的一定点,且OP![]() 6,若点M,N分别是射线OA,OB上异于点O的动点,则△PMN周长的最小值是__________.
6,若点M,N分别是射线OA,OB上异于点O的动点,则△PMN周长的最小值是__________.
【答案】6;
【解析】
设点P关于OA的对称点为C,关于OB的对称点为D,当点M、N在CD上时,△PMN的周长最小.
解:分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OP、OC、OD、PM、PN.
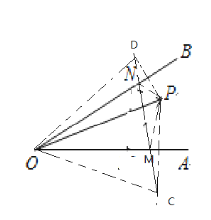
∵点P关于OA的对称点为C,关于OB的对称点为D,
∴PM=CM,OP=OC,∠COA=∠POA;
∵点P关于OB的对称点为D,
∴PN=DN,OP=OD,∠DOB=∠POB,
∴OC=OD=OP=6cm,∠COD=∠COA+∠POA+∠POB+∠DOB=2∠POA+2∠POB=2∠AOB=60°,
∴△COD是等边三角形,
∴CD=OC=OD=6.
∴△PMN的周长的最小值=PM+MN+PN=CM+MN+DN≥CD=6.
故答案为:6.


科目:初中数学 来源: 题型:
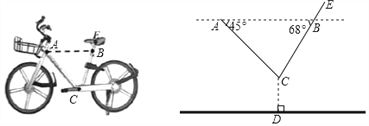
【题目】如图,一辆摩拜单车放在水平的地面上,车把头下方A处与坐垫下方B处在平行于地面的水平线上,A、B之间的距离约为49cm,现测得AC、BC与AB的夹角分别为45°与68°,若点C到地面的距离CD为28cm,坐垫中轴E处与点B的距离BE为4cm,求点E到地面的距离(结果保留一位小数).(参考数据:sin68°≈0.93,cos68°≈0.37,cot68°≈0.40)
查看答案和解析>>
科目:初中数学 来源: 题型:
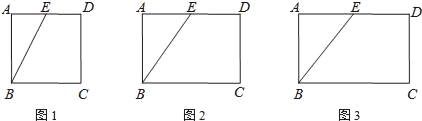
【题目】如图,在矩形ABCD中,E是AD的中点,点A关于BE的对称点为G(G在矩形ABCD内部),连接BG并延长交CD于F.
(1)如图1,当AB=AD时,
①根据题意将图1补全;
②直接写出DF和GF之间的数量关系.
(2)如图2,当AB≠AD时,如果点F恰好为DC的中点,求![]() 的值.
的值.
(3)如图3,当AB≠AD时,如果DC=nDF,写出求![]() 的值的思路(不必写出计算结果).
的值的思路(不必写出计算结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c经过点(﹣1,0),以下结论:①2a+b>0;②a+c<0;③4a+2b+c>0;④b2﹣5a2>2ac.其中正确的是( )
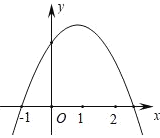
A. ①②B. ③④C. ②③④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC和△CDE都是等腰直角三角形,∠ACB=∠DCE=90°,且点A在ED的延长线上,以DE为直径的⊙O与AB交于G、H两点,连接BE.
(1)求证:BE是⊙O的切线;
(2)如图②,连接OB、OC,若tan∠CAD=![]() ,试判断四边形BECO的形状,请说明理由;
,试判断四边形BECO的形状,请说明理由;
(3)在(2)的条件下,若BF=![]() ,请你求出HG的长.
,请你求出HG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小方与小辉在玩军棋游戏,他们定义了一种新的规则,用军棋中的“工兵”、“连长”、“地雷”比较大小,共有6个棋子,分别为1个“工兵”,2个“连长”,3个“地雷”游戏规则如下:①游戏时,将棋反面朝上,两人随机各摸一个棋子进行比赛,先摸者摸出的棋不放回;②“工兵”胜“地雷”,“地雷”胜“连长”,“连长”胜“工兵”;③相同棋子不分胜负.
(1)若小方先摸,则小方摸到“排长”的事件是 ;若小方先摸到了“连长”,小辉在剩余的5个棋子中随机摸一个,则这一轮中小方胜小辉的概率为 .
(2)如果先拿走一个“连长”,在剩余的5个棋子中小方先摸一个棋子,然后小辉在剩余的4个棋子中随机摸一个,求这一轮中小方获胜的概率 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=x+1的图象l与y轴交于点C,A1的坐标为(1,0),点B1在直线l上,且A1B1平行于y轴,连接CA1、OB1交于点P1,过点A1作A1B2∥OB1交直线l于点B2,过点B1作B1A2∥CA1交x轴于点A2,A1B2与B1A2交于点P2,……,按此进行下去,则点P2019的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,已知点A(﹣3,0),B(0,4),对△OAB连续作旋转变换,依次得到△1,△2,△3,△4,…,则△2019的直角顶点的坐标为( )
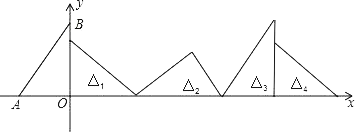
A. (8076,0)B. (8064,0)C. (8076,![]() )D. (8064,
)D. (8064,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图,在平面直角坐标系中,已知抛物线![]() 与x轴交于A,B两点,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(-2,0),(6,-8).
与x轴交于A,B两点,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(-2,0),(6,-8).

(1)求抛物线的函数表达式,并分别求出点B和点E的坐标;
(2)试探究抛物线上是否存在点F,使![]() ≌
≌![]() ,若存在,请直接写出点F的坐标;若不存在,请说明理由;
,若存在,请直接写出点F的坐标;若不存在,请说明理由;
(3)若点P是y轴负半轴上的一个动点,设其坐标为(0,m),直线PB与直线l交于点Q.试探究:当m为何值时,![]() 是等腰三角形.
是等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com