
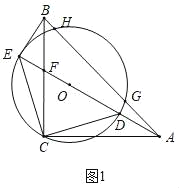
【题目】如图①,△ABC和△CDE都是等腰直角三角形,∠ACB=∠DCE=90°,且点A在ED的延长线上,以DE为直径的⊙O与AB交于G、H两点,连接BE.
(1)求证:BE是⊙O的切线;
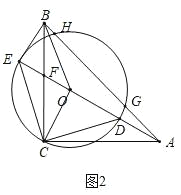
(2)如图②,连接OB、OC,若tan∠CAD=![]() ,试判断四边形BECO的形状,请说明理由;
,试判断四边形BECO的形状,请说明理由;
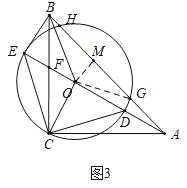
(3)在(2)的条件下,若BF=![]() ,请你求出HG的长.
,请你求出HG的长.

【答案】(1)证明见解析;(2)四边形BECO是平行四边形;(3)HG=![]() .
.
【解析】
(1)利用等腰直角三角形的性质,证△BCE≌△ACD,推出∠CBE=∠CAD,证出∠AEB=90°,即可推出结论;
(2)先证CO⊥DE,AO=2CO,推出AD=CO,由△BCE≌△ACD可知BE=AD,所以BE=CO,再证BE∥CO即可;
(3)先由平行四边形的性质推出对角线CB的长,利用三角函数求出AB的长,再在Rt△AOC中求出AO,CO的长,过点O作OM⊥AB于点M,连接OG,证△MAO∽△BAE,求出OM的长,由勾股定理求出MG的长,可进一步推出HG的长.
(1)证明:∵△ABC和△CDE都是等腰直角三角形,
∴BC=AC,EC=DC,
∴∠DCE=∠ACB=90°,
∴∠DCE﹣∠FCD=∠ACB﹣∠FCD,
∴∠BCE=∠ACD,
∴△BCE≌△ACD(SAS),
∴∠CBE=∠CAD,
∴∠ABE+∠BAE=90°,
∴∠AEB=90°,
∴BE⊥OE,
又∵OE是⊙O的半径,
∴BE是⊙O的切线;
(2)四边形BECO是平行四边形,
理由如下:
∵点O是ED的中点,
∴CO是DE边上的中线,
∵△CDE是等腰三角形,
∴CO是DE边上的高线,
∴CO⊥DE,
∴∠COE=∠AOC=90°,
∵∠AEB=90°,
∴∠AEB=COE,
∴CO∥BE,
∵在Rt△AOC中,tan∠CAD=![]() ,
,
∴![]() =
=![]() ,
,
∴AO=2CO,
∴DO=CO,
∴AD=CO,
∵△BCE≌△ACD,
∴BE=AD,
∴BE=CO,
∴四边形BECO是平行四边形;
(3)∵四边形BECO是平行四边形,
∴CF=BF=![]() ,
,
∴BC=2![]() ,
,
∴AC=BC=2![]() ,
,
∴AB=![]() =2
=2![]() ,
,
设OC=x,则AO=2x,
∵在Rt△AOC中,OC2+AO2=AC2,
∴x2+(2x)2=(2![]() )2,
)2,
解得,x=2(取正值),
∴OC=BE=2,AO=4,
如图3,过点O作OM⊥AB于点M,连接OG,
∴∠AMO=90°,HG=2MG,
∴∠AMO=∠AEB=90°,
∵∠MAO=∠BAE,
∴△MAO∽△BAE,
∴![]() ,
,
∴![]() ,
,
∴OM=![]() ,
,
在Rt△MOG中,OM2+MG2=OG2,
∴(![]() )2+MG2=22,
)2+MG2=22,
∴MG=![]() (取正值),
(取正值),
∴HG=2MG=![]() .
.


科目:初中数学 来源: 题型:
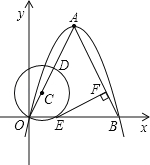
【题目】如图,已知A(2,4),以A为顶点的抛物线经过原点交x轴于B.
(1)求抛物线解析式;
(2)取OA上一点D,以OD为直径作⊙C交x轴于E,作EF⊥AB于F,求证EF是⊙C的切线;
(3)设⊙C半径为r,EF=m,求m与r的函数关系式及自变量r的取值范围;
(4)当⊙C与AB相切时,求⊙C半径r的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
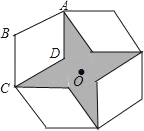
【题目】为了庆祝“六一儿童节”,六年级同学在班会课进行了趣味活动.小舟同学在模板上画出一个菱形ABCD,将它以点O为中心按顺时针方向分别旋转90°,180°,270°后得到如图所示的图形,其中∠ABC=120°,AB=2cm,然后小舟将此图形制作成一个靶子,那么当我们投飞镖时命中阴影部分的概率为( )
A. ![]() B. 2﹣
B. 2﹣![]() C.
C. ![]() -1D.
-1D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
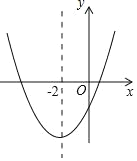
【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,顶点坐标为(﹣2,﹣9a),下列结论:①abc>0;②4a+2b+c>0;③5a﹣b+c=0;④若方程a(x+5)(x﹣1)=﹣1有两个根x1和x2,且x1<x2,则﹣5<x1<x2<1;⑤若方程|ax2+bx+c|=2有四个根,则这四个根的和为﹣4.其中正确的结论有( )
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
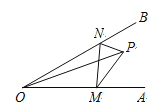
【题目】如图,∠AOB![]() 30°,点P是∠AOB内的一定点,且OP
30°,点P是∠AOB内的一定点,且OP![]() 6,若点M,N分别是射线OA,OB上异于点O的动点,则△PMN周长的最小值是__________.
6,若点M,N分别是射线OA,OB上异于点O的动点,则△PMN周长的最小值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
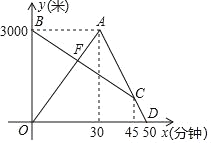
【题目】某个周末,小丽从家去园博园参观,同时妈妈参观结束从园博园回家,小丽刚到园博园就发现要下雨,于是立即按原路返回,追上妈妈后,两人一同回家(小丽和妈妈始终在同一条笔直的公路上行走)如图是两人离家的距离y(米)与小丽出发的时间x(分)之间的函数图象,请根据图象信息回答下列问题:
(1)求线段BC的解析式;
(2)求点F的坐标,并说明其实际意义;
(3)与按原速度回家相比,妈妈提前了几分钟到家?并直接写出小丽与妈妈何时相距800米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某手机店销售一部A型手机比销售一部B型手机获得的利润多50元,销售相同数量的A型手机和B型手机获得的利润分别为3000元和2000元.
(1)求每部A型手机和B型手机的销售利润分别为多少元?
(2)该商店计划一次购进两种型号的手机共110部,其中A型手机的进货量不超过B型手机的2倍.设购进B型手机n部,这110部手机的销售总利润为y元.
①求y关于n的函数关系式;
②该手机店购进A型、B型手机各多少部,才能使销售总利润最大?
(3)实际进货时,厂家对B型手机出厂价下调m(30<m<100)元,且限定商店最多购进B型手机80台.若商店保持两种手机的售价不变,请你根据以上信息及(2)中的条件,设计出使这110部手机销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016山西省)我省某苹果基地销售优质苹果,该基地对需要送货且购买量在2000kg﹣5000kg(含2000kg和5000kg)的客户有两种销售方案(客户只能选择其中一种方案):
方案A:每千克5.8元,由基地免费送货.
方案B:每千克5元,客户需支付运费2000元.
(1)请分别写出按方案A,方案B购买这种苹果的应付款y(元)与购买量x(kg)之间的函数表达式;
(2)求购买量x在什么范围时,选用方案A比方案B付款少;
(3)某水果批发商计划用20000元,选用这两种方案中的一种,购买尽可能多的这种苹果,请直接写出他应选择哪种方案.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com