
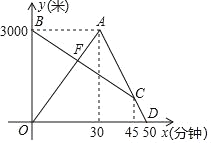
【题目】某个周末,小丽从家去园博园参观,同时妈妈参观结束从园博园回家,小丽刚到园博园就发现要下雨,于是立即按原路返回,追上妈妈后,两人一同回家(小丽和妈妈始终在同一条笔直的公路上行走)如图是两人离家的距离y(米)与小丽出发的时间x(分)之间的函数图象,请根据图象信息回答下列问题:
(1)求线段BC的解析式;
(2)求点F的坐标,并说明其实际意义;
(3)与按原速度回家相比,妈妈提前了几分钟到家?并直接写出小丽与妈妈何时相距800米.
【答案】(1)y=﹣50x+3000;(2)点F的坐标为(20,2000),其实际意义为:小丽出发20分钟时,在离家2000米处与妈妈相遇;(3)妈妈提前了10分钟到家,小丽与妈妈相距800米的时间是![]() 分钟,
分钟,![]() 分钟和37分钟.
分钟和37分钟.
【解析】
(1)由图象可知,点A(30,3000),点D(50,0),用待定系数法求出AD的解析式,再将C点横坐标代入即可求得点C的纵坐标,再由点B(0,3000),同样可由待定系数法求得BC的解析式;
(2)待定系数法求出OA的解析式,然后将其与BC的解析式联立,可求得点F的坐标,进而得其实际意义;
(3)求出直线BC与x轴交点的横坐标,再与x等于50相比较即可得妈妈提前回家的时间;小丽与妈妈相距800米有三种可能,分别求出即可.
解:(1)由图象可知,点A(30,3000),点D(50,0)
设线段AD的解析式为:y=kx+b,将点A,点D坐标代入得![]() ,
,
解得![]() ,
,
∴y=﹣150x+7500.
将x=45代入上式得y=750,
∴点C坐标为(45,750).
设线段BC的解析式为y=mx+n,将(0,3000)和(45,750)代入得:
![]() ,解得
,解得![]() ,
,
∴y=﹣50x+3000.
答:线段BC的解析式为y=﹣50x+3000.
(2)设OA的解析式为y=px,将点A(30,3000)代入得:3000=30p,
∴p=100,
∴y=100x.
由![]() 解得
解得![]() ,
,
∴点F的坐标为(20,2000),其实际意义为:小丽出发20分钟时,在离家2000米处与妈妈相遇.
(3)在y=﹣50x+3000中,令y=0得:0=﹣50x+3000,
∴x=60,
60﹣50=10,
∴妈妈提前了10分钟到家.
由|100x﹣(﹣50x+3000)|=800,得:x=![]() 或x=
或x=![]() ;
;
由(﹣150x+7500)﹣(﹣50x+3000)=800,得x=37.
答:妈妈提前了10分钟到家,小丽与妈妈相距800米的时间是![]() 分钟,
分钟,![]() 分钟和37分钟.
分钟和37分钟.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
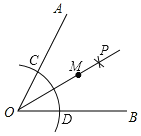
【题目】如图所示,∠AOB=70°,以点O为圆心,以适当长为半径作弧分别交OA,OB于C,D两点;分别以C,D为圆心,以大于![]() CD的长为半径作弧,两弧相交于点P;以O为端点作射线OP,在射线OP上取点M,连接MC、MD.若测得∠CMD=40°,则∠MDB=_____
CD的长为半径作弧,两弧相交于点P;以O为端点作射线OP,在射线OP上取点M,连接MC、MD.若测得∠CMD=40°,则∠MDB=_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2﹣(2k﹣1)x+k2+1=0有两个不相等的实数根x1,x2.
(1)求实数k的取值范围;
(2)若方程的两实数根x1,x2满足|x1|+|x2|=x1x2,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC和△CDE都是等腰直角三角形,∠ACB=∠DCE=90°,且点A在ED的延长线上,以DE为直径的⊙O与AB交于G、H两点,连接BE.
(1)求证:BE是⊙O的切线;
(2)如图②,连接OB、OC,若tan∠CAD=![]() ,试判断四边形BECO的形状,请说明理由;
,试判断四边形BECO的形状,请说明理由;
(3)在(2)的条件下,若BF=![]() ,请你求出HG的长.
,请你求出HG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
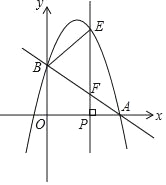
【题目】如图,在平面直角坐标系中,直线y=-![]() x+2分别交x轴、y轴于点A、B,抛物线y=﹣x2+bx+c经过点A、B.点P是x轴上一个动点,过点P作垂直于x轴的直线分别交抛物线和直线AB于点E和点F.设点P的横坐标为m.
x+2分别交x轴、y轴于点A、B,抛物线y=﹣x2+bx+c经过点A、B.点P是x轴上一个动点,过点P作垂直于x轴的直线分别交抛物线和直线AB于点E和点F.设点P的横坐标为m.
(1)点A的坐标为 .
(2)求这条抛物线所对应的函数表达式.
(3)点P在线段OA上时,若以B、E、F为顶点的三角形与△FPA相似,求m的值.
(4)若E、F、P三个点中恰有一点是其它两点所连线段的中点(三点重合除外),称E、F、P三点为“共谐点”.直接写出E、F、P三点成为“共谐点”时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=x+1的图象l与y轴交于点C,A1的坐标为(1,0),点B1在直线l上,且A1B1平行于y轴,连接CA1、OB1交于点P1,过点A1作A1B2∥OB1交直线l于点B2,过点B1作B1A2∥CA1交x轴于点A2,A1B2与B1A2交于点P2,……,按此进行下去,则点P2019的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于![]() 的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )
的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )

A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A,交AB于点D,交CA的延长线于点E,过点E作AB的平行线交⊙A于点F,连接AF,BF,DF.
(1)求证:△ABC≌△ABF;
(2)填空:
①当∠CAB= °时,四边形ADFE为菱形;
②在①的条件下,BC= cm时,四边形ADFE的面积是6![]() cm2.
cm2.

查看答案和解析>>
科目:初中数学 来源: 题型:
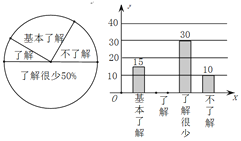
【题目】济南市某中学对部分学生就食品安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有_____人,扇形统计围中“基本了解”部分所对应扇形的圆心角为______°;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对食品安全知识达到“了解”和“基本了解”程度的总人数;
(4)从对食品安全知识达到“了解”的3个女生和2个男生中随机抽取2人参加食品安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com