
ЁОЬтФПЁПМУФЯЪаФГжабЇЖдВПЗжбЇЩњОЭЪГЦЗАВШЋжЊЪЖЕФСЫНтГЬЖШЃЌВЩгУЫцЛњГщбљЕїВщЕФЗНЪНЃЌВЂИљОнЪеМЏЕНЕФаХЯЂНјааЭГМЦЃЌЛцжЦСЫЯТУцСНЗљЩаВЛЭъећЕФЭГМЦЭМ.ЧыФуИљОнЭГМЦЭМжаЫљЬсЙЉЕФаХЯЂНтД№ЯТСаЮЪЬтЃК
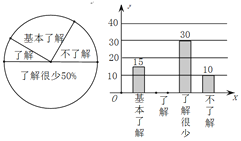
ЃЈ1ЃЉНгЪмЮЪОэЕїВщЕФбЇЩњЙВга_____ШЫЃЌЩШаЮЭГМЦЮЇжаЁАЛљБОСЫНтЁБВПЗжЫљЖдгІЩШаЮЕФдВаФНЧЮЊ______ЁуЃЛ
ЃЈ2ЃЉЧыВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉШєИУжабЇЙВгабЇЩњ900ШЫЃЌЧыИљОнЩЯЪіЕїВщНсЙћЃЌЙРМЦИУжабЇбЇЩњжаЖдЪГЦЗАВШЋжЊЪЖДяЕНЁАСЫНтЁБКЭЁАЛљБОСЫНтЁБГЬЖШЕФзмШЫЪ§ЃЛ
ЃЈ4ЃЉДгЖдЪГЦЗАВШЋжЊЪЖДяЕНЁАСЫНтЁБЕФ3ИіХЎЩњКЭ2ИіФаЩњжаЫцЛњГщШЁ2ШЫВЮМгЪГЦЗАВШЋжЊЪЖОКШќЃЌЧыгУЪїзДЭМЛђСаБэЗЈЧѓГіЧЁКУГщЕН1ИіФаЩњКЭ1ИіХЎЩњЕФИХТЪЃЎ
ЁОД№АИЁП(1)60, 90ЃЛ(2)5ЃЛ(3)300ЃЛ (4) ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉгУЁАСЫНтКмЩйЁБВПЗжЕФШЫЪ§Г§вдЫќЫљеМЕФАйЗжБШПЩЕУЕНЕїВщЕФзмШЫЪ§ЃЛШЛКѓгУЁАЛљБОСЫНтЁБВПЗжЫљеМЕФБШР§ГЫвд360ЁуЕУЕНЩШаЮЭГМЦЭМжаЁАЛљБОСЫНтЁБВПЗжЫљЖдгІЩШаЮЕФдВаФНЧЕФЖШЪ§ЃЛ
ЃЈ2ЃЉЯШМЦЫуГіЁАСЫНтЁБВПЗжЕФШЫЪ§ЃЌШЛКѓВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉРћгУбљБОЙРМЦзмЬхЃЌгУ900ГЫвдЁАСЫНтЁБКЭЁАЛљБОСЫНтЁБЫљеМЕФАйЗжБШЕФКЭМДПЩЃЛ
ЃЈ4ЃЉЛЪїзДЭМЮЊЃЈЗжБ№гУAЁЂBБэЪОСНУћХЎЩњЃЌгУCЁЂDБэЪОСНУћФаЩњЃЉеЙЪОЫљга12жжЕШПЩФмЕФНсЙћЪ§ЃЌдйевГіЧЁКУГщЕН1ИіФаЩњКЭ1ИіХЎЩњЕФНсЙћЪ§ЃЌШЛКѓИљОнИХТЪЙЋЪНЧѓНтЃЎ
ЃЈ1ЃЉ30ЁТ50%=60ЃЌ
ЫљвдНгЪмЮЪОэЕїВщЕФбЇЩњЙВга60ШЫЃЛ
ЩШаЮЭГМЦЭМжаЁАЛљБОСЫНтЁБВПЗжЫљЖдгІЩШаЮЕФдВаФНЧЕФЖШЪ§ЮЊ![]() ЃЛ
ЃЛ
ЙЪД№АИЮЊ60ЃЛ90ЁуЃЛ
ЃЈ2ЃЉЁАСЫНтЁБВПЗжЕФШЫЪ§=60-15-30-10=5ЃЌ
ЬѕаЮЭГМЦЭМЮЊЃК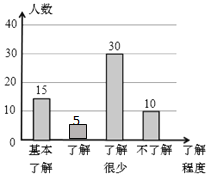 ЃЌ
ЃЌ
![]()
ЫљвдЙРМЦИУжабЇбЇЩњжаЖдЪГЦЗАВШЋжЊЪЖДяЕНЁАСЫНтЁБКЭЁАЛљБОСЫНтЁБГЬЖШЕФзмШЫЪ§ЮЊ300ШЫЃЛ
ЃЈ4ЃЉЛЪїзДЭМЮЊЃКЃЈЗжБ№гУAЁЂBБэЪОСНУћХЎЩњЃЌгУCЁЂDБэЪОСНУћФаЩњЃЉ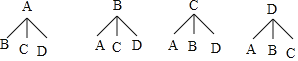
ЙВга12жжЕШПЩФмЕФНсЙћЪ§ЃЌЦфжаЧЁКУГщЕН1ИіФаЩњКЭ1ИіХЎЩњЕФНсЙћЪ§ЮЊ8ЃЌ
ЫљвдЧЁКУГщЕН1ИіФаЩњКЭ1ИіХЎЩњЕФИХТЪ= ![]() ЃЎ
ЃЎ


 УЯНЈЦНаЁбЇЙіЖЏВтЪдЯЕСаД№АИ
УЯНЈЦНаЁбЇЙіЖЏВтЪдЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
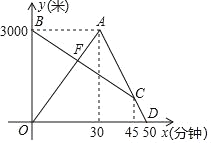
ЁОЬтФПЁПФГИіжмФЉЃЌаЁРіДгМвШЅдАВЉдАВЮЙлЃЌЭЌЪБТшТшВЮЙлНсЪјДгдАВЉдАЛиМвЃЌаЁРіИеЕНдАВЉдАОЭЗЂЯжвЊЯТгъЃЌгкЪЧСЂМДАДдТЗЗЕЛиЃЌзЗЩЯТшТшКѓЃЌСНШЫвЛЭЌЛиМв(аЁРіКЭТшТшЪМжедкЭЌвЛЬѕБЪжБЕФЙЋТЗЩЯаазп)ШчЭМЪЧСНШЫРыМвЕФОрРыy(Уз)гыаЁРіГіЗЂЕФЪБМфx(Зж)жЎМфЕФКЏЪ§ЭМЯѓЃЌЧыИљОнЭМЯѓаХЯЂЛиД№ЯТСаЮЪЬтЃК
(1)ЧѓЯпЖЮBCЕФНтЮіЪНЃЛ
(2)ЧѓЕуFЕФзјБъЃЌВЂЫЕУїЦфЪЕМЪвтвхЃЛ
(3)гыАДдЫйЖШЛиМвЯрБШЃЌТшТшЬсЧАСЫМИЗжжгЕНМвЃПВЂжБНгаДГіаЁРігыТшТшКЮЪБЯрОр800УзЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
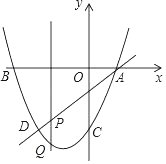
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНx2+bxЉ3Й§ЕуAЃЈ1ЃЌ0ЃЉЃЌжБЯпADНЛХзЮяЯпгкЕуDЃЌЕуDЕФКсзјБъЮЊЉ2ЃЌЕуPЪЧЯпЖЮADЩЯЕФЖЏЕуЃЎ
ЃЈ1ЃЉbЃНЁЁ ЁЁЃЌХзЮяЯпЕФЖЅЕузјБъЮЊЁЁ ЁЁЃЛ
ЃЈ2ЃЉЧѓжБЯпADЕФНтЮіЪНЃЛ
ЃЈ3ЃЉЙ§ЕуPЕФжБЯпДЙжБгкxжсЃЌНЛХзЮяЯпгкЕуQЃЌСЌНгAQЃЌDQЃЌЕБЁїADQЕФУцЛ§ЕШгкЁїABDЕФУцЛ§ЕФвЛАыЪБЃЌЧѓЕуQЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ2016ЩНЮїЪЁЃЉЮвЪЁФГЦЛЙћЛљЕиЯњЪлгХжЪЦЛЙћЃЌИУЛљЕиЖдашвЊЫЭЛѕЧвЙКТђСПдк2000kgЉ5000kgЃЈКЌ2000kgКЭ5000kgЃЉЕФПЭЛЇгаСНжжЯњЪлЗНАИЃЈПЭЛЇжЛФмбЁдёЦфжавЛжжЗНАИЃЉЃК
ЗНАИAЃКУПЧЇПЫ5.8дЊЃЌгЩЛљЕиУтЗбЫЭЛѕЃЎ
ЗНАИBЃКУПЧЇПЫ5дЊЃЌПЭЛЇашжЇИЖдЫЗб2000дЊЃЎ
ЃЈ1ЃЉЧыЗжБ№аДГіАДЗНАИAЃЌЗНАИBЙКТђетжжЦЛЙћЕФгІИЖПюyЃЈдЊЃЉгыЙКТђСПxЃЈkgЃЉжЎМфЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉЧѓЙКТђСПxдкЪВУДЗЖЮЇЪБЃЌбЁгУЗНАИAБШЗНАИBИЖПюЩйЃЛ
ЃЈ3ЃЉФГЫЎЙћХњЗЂЩЬМЦЛЎгУ20000дЊЃЌбЁгУетСНжжЗНАИжаЕФвЛжжЃЌЙКТђОЁПЩФмЖрЕФетжжЦЛЙћЃЌЧыжБНгаДГіЫћгІбЁдёФФжжЗНАИЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПХзЮяЯпy=ax2+bx+cЕФЖЅЕуЮЊDЃЈЈC1ЃЌ2ЃЉЃЌгыxжсЕФвЛИіНЛЕуAдкЕуЃЈЈC3ЃЌ0ЃЉКЭЃЈЈC2ЃЌ0ЃЉжЎМфЃЌЦфВПЗжЭМЯѓШчЯТЭМЃЌдђвдЯТНсТлЃКЂйb2ЈC4ac<0ЃЛЂкa+b+c<0ЃЛЂлcЈCa=2ЃЛЂмЗНГЬax2+bx+cЈC2=0гаСНИіЯрЕШЕФЪЕЪ§ИљЃЎЦфжае§ШЗНсТлЕФИіЪ§ЮЊЃЈ ЃЉ

A. 1Иі B. 2Иі C. 3Иі D. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
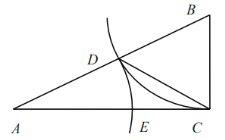
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯACB=90ЁуЃЌвдЕуBЮЊдВаФЃЌBCГЄЮЊАыОЖЛЛЁЃЌНЛБпABгыЕуDЃЌвдAЮЊдВаФЃЌADГЄЮЊАыОЖЛЛЁЃЌНЛБпACгкЕуEЃЌСЌНгCDЃЎ
ЃЈ1ЃЉШєЁЯA=28ЁуЃЌЧѓЁЯACDЕФЖШЪ§ЃЛ
ЃЈ2ЃЉЩшBC=aЃЌAC=bЃЎ
ЂйЯпЖЮADЕФГЄЪЧЗНГЬ![]() ЕФвЛИіИљТ№ЃПЮЊЪВУДЃП
ЕФвЛИіИљТ№ЃПЮЊЪВУДЃП
ЂкШєAD=ECЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
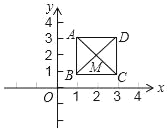
ЁОЬтФПЁПШчЭМЃЌвбжЊе§ЗНаЮABCDЃЌЖЅЕуAЃЈ1ЃЌ3ЃЉЁЂBЃЈ1ЃЌ1ЃЉЁЂCЃЈ3ЃЌ1ЃЉЃЎЙцЖЈЁААбе§ЗНаЮABCDЯШбиxжсЗелЃЌдйЯђзѓЦНвЦвЛИіЕЅЮЛЁБЮЊвЛДЮБфЛЛЃЎШчДЫетбљЃЌСЌајОЙ§2018ДЮБфЛЛКѓЃЌе§ЗНаЮABCDЕФЖдНЧЯпНЛЕуMЕФзјБъЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌХзЮяЯп
жаЃЌХзЮяЯп![]() ЃЈ
ЃЈ![]() ЃЉгы
ЃЉгы![]() жсНЛгк
жсНЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЈЕу
СНЕуЃЈЕу![]() дкЕу
дкЕу![]() зѓВрЃЉЃЌгы
зѓВрЃЉЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌИУХзЮяЯпЕФЖЅЕу
ЃЌИУХзЮяЯпЕФЖЅЕу![]() ЕФзнзјБъЪЧ
ЕФзнзјБъЪЧ![]() .
.

ЃЈ1ЃЉЧѓЕу![]() ЁЂ
ЁЂ![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ2ЃЉЩшжБЯпгыжБЯп![]() ЙигкИУХзЮяЯпЕФЖдГЦжсЖдГЦЃЌЧѓжБЯпЕФБэДяЪНЃЛ
ЙигкИУХзЮяЯпЕФЖдГЦжсЖдГЦЃЌЧѓжБЯпЕФБэДяЪНЃЛ
ЃЈ3ЃЉЦНаагк![]() жсЕФжБЯп
жсЕФжБЯп![]() гыХзЮяЯпНЛгкЕу
гыХзЮяЯпНЛгкЕу![]() ЁЂ
ЁЂ![]() ,гыжБЯпНЛгкЕу
,гыжБЯпНЛгкЕу![]() .Шє
.Шє![]() ЃЌНсКЯКЏЪ§ЭМЯѓЃЌЧѓ
ЃЌНсКЯКЏЪ§ЭМЯѓЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
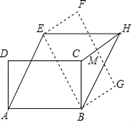
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDжаЃЌABЃН3ЃЌADЃН![]() ЃЌНЋОиаЮABCDШЦЕуBАДЫГЪБеыЗНЯђа§зЊКѓЕУЕНОиаЮEBGFЃЌДЫЪБЧЁКУЫФБпаЮAEHBЮЊСтаЮЃЌСЌНгCHНЛFGгкЕуMЃЌдђHMЃНЃЈЁЁЁЁЃЉ
ЃЌНЋОиаЮABCDШЦЕуBАДЫГЪБеыЗНЯђа§зЊКѓЕУЕНОиаЮEBGFЃЌДЫЪБЧЁКУЫФБпаЮAEHBЮЊСтаЮЃЌСЌНгCHНЛFGгкЕуMЃЌдђHMЃНЃЈЁЁЁЁЃЉ
A. ![]() B. 1 C.
B. 1 C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com