
【题目】抛物线y=ax2+bx+c的顶点为D(–1,2),与x轴的一个交点A在点(–3,0)和(–2,0)之间,其部分图象如下图,则以下结论:①b2–4ac<0;②a+b+c<0;③c–a=2;④方程ax2+bx+c–2=0有两个相等的实数根.其中正确结论的个数为( )

A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】试题分析:由抛物线与x轴有两个交点,可知b2-4ac>0,所以①错误;
由抛物线的顶点为D(-1,2),可知抛物线的对称轴为直线x=-1,然后由抛物线与x轴的一个交点A在点(-3,0)和(-2,0)之间,可知抛物线与x轴的另一个交点在点(0,0)和(1,0)之间,因此当x=1时,y<0,即a+b+c<0,所以②正确;
由抛物线的顶点为D(-1,2),可知a-b+c=2,然后由抛物线的对称轴为直线x=![]() =-1,可得b=2a,因此a-2a+c=2,即c-a=2,所以③正确;
=-1,可得b=2a,因此a-2a+c=2,即c-a=2,所以③正确;
由于当x=-1时,二次函数有最大值为2,即只有x=-1时,ax2+bx+c=2,因此方程ax2+bx+c-2=0有两个相等的实数根,所以④正确.
故选:C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,点E在AB上,把△ABC沿CE折叠后,点B恰好与斜边AC的中点D重合.
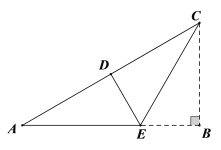
(1)求证:△ACE为等腰三角形;
(2)若AB=6,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要建一个如图所示的面积为300![]() 的长方形围栏,围栏总长50m,一边靠墙(墙长25m),
的长方形围栏,围栏总长50m,一边靠墙(墙长25m),

(1)求围栏的长和宽;
(2)能否围成面积为400 ![]() 的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由。
的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义![]() 表示不大于x的最大整数,例如
表示不大于x的最大整数,例如![]() ,
,![]() ,
,![]() .
.
(1)将![]() 、
、![]() 、
、![]() 按照从小到大的顺序用不等号连接:_______________;
按照从小到大的顺序用不等号连接:_______________;
(2)利用(1)中的结论,方程![]() 的解为___________________.
的解为___________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是二次函数![]() 图象的一部分,图象过点
图象的一部分,图象过点![]() ,二次函数图象对称轴为直线
,二次函数图象对称轴为直线![]() ,给出五个结论:①
,给出五个结论:①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() 随
随![]() 的增大而增大;④方程
的增大而增大;④方程![]() 的根为
的根为![]() ,
,![]() ;⑤
;⑤![]() 其中正确结论是( )
其中正确结论是( )

A. ①②③ B. ①③④ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售某种玩具,进货价为![]() 元.根据市场调查:在一段时间内,销售单价是
元.根据市场调查:在一段时间内,销售单价是![]() 元时,销售量是
元时,销售量是![]() 件,而销售单价每上涨
件,而销售单价每上涨![]() 元,就会少售出
元,就会少售出![]() 件玩具,超市要完成不少于
件玩具,超市要完成不少于![]() 件的销售任务,又要获得最大利润,则销售单价应定为________元.
件的销售任务,又要获得最大利润,则销售单价应定为________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
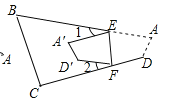
【题目】(问题探究)
将三角形![]() 纸片沿
纸片沿![]() 折叠,使点A落在点
折叠,使点A落在点![]() 处.
处.
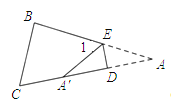
(1)如图,当点A落在四边形![]() 的边
的边![]() 上时,直接写出
上时,直接写出![]() 与
与![]() 之间的数量关系;
之间的数量关系;
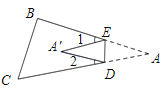
(2)如图,当点A落在四边形![]() 的内部时,求证:
的内部时,求证:![]() ;
;
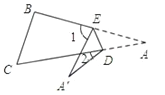
(3)如图,当点A落在四边形![]() 的外部时,探索
的外部时,探索![]() ,
,![]() ,
,![]() 之间的数量关系,并加以证明;
之间的数量关系,并加以证明;
(拓展延伸)
(4)如图,若把四边形![]() 纸片沿
纸片沿![]() 折叠,使点A、D落在四边形
折叠,使点A、D落在四边形![]() 的内部点
的内部点![]() 、
、![]() 的位置,请你探索此时
的位置,请你探索此时![]() ,
,![]() ,
,![]() ,
,![]() 之间的数量关系,写出你发现的结论,并说明理由.
之间的数量关系,写出你发现的结论,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
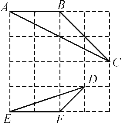
【题目】如图,在4×4的正方形网格中,△ABC和△DEF的顶点都在边长为1的正方形的顶点上.
(1)填空:∠ABC=__________度,BC=_________;
(2)求证:∠C=∠E.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).

(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△![]() C;平移△ABC,若A的对应点
C;平移△ABC,若A的对应点![]() 的坐标为(0,4),画出平移后对应的△
的坐标为(0,4),画出平移后对应的△![]() ;
;
(2)若将△![]() C绕某一点旋转可以得到△
C绕某一点旋转可以得到△![]() ,请直接写出旋转中心的坐标;
,请直接写出旋转中心的坐标;
(3)在![]() 轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com