
【题目】如图所示是二次函数![]() 图象的一部分,图象过点
图象的一部分,图象过点![]() ,二次函数图象对称轴为直线
,二次函数图象对称轴为直线![]() ,给出五个结论:①
,给出五个结论:①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() 随
随![]() 的增大而增大;④方程
的增大而增大;④方程![]() 的根为
的根为![]() ,
,![]() ;⑤
;⑤![]() 其中正确结论是( )
其中正确结论是( )

A. ①②③ B. ①③④ C. ②③④ D. ③④⑤
【答案】B
【解析】
通过观察图象,①二次函数图象的对称轴为直线x=1,所以x=﹣![]() =1>0,又因为二次函数的开口向下,得出a<0,所以b>0,二次函数与y轴交于x轴上方,所以c>0,得出bc>0;
=1>0,又因为二次函数的开口向下,得出a<0,所以b>0,二次函数与y轴交于x轴上方,所以c>0,得出bc>0;
②由图象可看出当x=1时,y=a+b+c>0;
③根据二次函数的单调性进行判断;
④因为对称轴为x=1,且方程的一个根为x2=3,另一个根x1=﹣1;
⑤因为二次函数与x轴的两个交点是(﹣1,0)(3,0),且开口向下,所以当x=﹣2时,y=4a﹣2b+c<0.
①由图象可看出抛物线的开口向下,∴a<0,由对称轴x=﹣![]() =1>0,得b>0,抛物线与y轴的交点在x轴上方,∴c>0,即得bc>0,故①正确.
=1>0,得b>0,抛物线与y轴的交点在x轴上方,∴c>0,即得bc>0,故①正确.
②由图象可看出当x=1时,y=a+b+c>0,故②不正确.
③由对称轴x=1,及二次函数的单调性可知:当x<1时,y随着x的增大而增大,故③正确.
④因为对称轴为x=1,且方程的一个根为x2=3,∴![]() =1,另一个根x1=﹣1,故④正确.
=1,另一个根x1=﹣1,故④正确.
⑤因为二次函数与x轴的两个交点是(﹣1,0)(3,0),且开口向下,∴当x=﹣2时,y=4a﹣2b+c<0,故⑤不正确.
故选B.


科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,D是AB的中点,过点B作∠CBE=∠A,BE与射线CA相交于点E,与射线CD相交于点F.
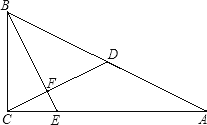
(1)如图,当点E在线段CA上时,求证:BE⊥CD;
(2)若BE=CD,那么线段AC与BC之间具有怎样的数量关系?并证明你所得到的结论;
(3)若△BDF是等腰三角形,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某地火车站及周围的简单平面图.(每个小正方形的边长代表1千米.)
(1)请以火车站所在的位置为坐标原点,建立平面直角坐标系,并表示出体育场A、超市B市场C、文化宫D的坐标.
(2)在这个坐标平面内,连接OA,若∠AOB的度数大约为53°,请利用所给数据描述体育场相对于火车站的位置.
(3)要想用第(2)问的方法描述文化宫在火车站的什么位置,需要测量哪些数据?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点![]() 是正比例函数
是正比例函数![]() 与反比例函数
与反比例函数![]() 的图象在第一象限的交点,
的图象在第一象限的交点,![]() 轴,垂足为点
轴,垂足为点![]() ,
,![]() 的面积是2.
的面积是2.

(1)求![]() 的值以及这两个函数的解析式;
的值以及这两个函数的解析式;
(2)若点![]() 在
在![]() 轴上,且
轴上,且![]() 是以
是以![]() 为腰的等腰三角形,求点
为腰的等腰三角形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场投入13 800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
类别/单价 | 成本价 | 销售价(元/箱) |
甲 | 24 | 36 |
乙 | 33 | 48 |
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的顶点为D(–1,2),与x轴的一个交点A在点(–3,0)和(–2,0)之间,其部分图象如下图,则以下结论:①b2–4ac<0;②a+b+c<0;③c–a=2;④方程ax2+bx+c–2=0有两个相等的实数根.其中正确结论的个数为( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F。

(1)求证:△ABE≌△CAD;(2)求∠BFD的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,
,![]() ,
,![]() ,
,![]() .点
.点![]() 从
从![]() 开始沿边
开始沿边![]() 向点
向点![]() 以
以![]() 的速度移动,与此同时,点
的速度移动,与此同时,点![]() 从点
从点![]() 开始沿边
开始沿边![]() 向点
向点![]() 以
以![]() 的速度移动.如果
的速度移动.如果![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,当点
同时出发,当点![]() 运动到点
运动到点![]() 时,两点停止运动,问:
时,两点停止运动,问:
![]() 经过几秒,
经过几秒,![]() 的面积等于
的面积等于![]() ?
?
(2)![]() 的面积会等于
的面积会等于![]() 吗?若会,请求出此时的运动时间;若不会,请说明理由.
吗?若会,请求出此时的运动时间;若不会,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com