
【题目】如图,在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A,交AB于点D,交CA的延长线于点E,过点E作AB的平行线交⊙A于点F,连接AF,BF,DF.
(1)求证:△ABC≌△ABF;
(2)填空:
①当∠CAB= °时,四边形ADFE为菱形;
②在①的条件下,BC= cm时,四边形ADFE的面积是6![]() cm2.
cm2.

【答案】(1)证明见解析;(2)60;(3)6.
【解析】
(1)首先利用平行线的性质得到∠FAB=∠CAB,然后利用SAS证得两三角形全等即可;
(2)当∠CAB=60°时,四边形ADFE为菱形,根据∠CAB=60°,得到∠FAB=∠CAB=∠CAB=60°,从而得到EF=AD=AE,利用邻边相等的平行四边形是菱形进行判断四边形ADFE是菱形;
(3)设菱形AEFD的边长为a,易知△AEF、△AFD都是等边三角形,列出方程求出a,再在RT△ACB中,利用勾股定理即可解决问题.
(1)证明:∵EF∥AB,
∴∠E=∠CAB,∠EFA=∠FAB,
∵∠E=∠EFA,
∴∠FAB=∠CAB,
在△ABC和△ABF中,
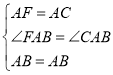 ,
,
∴△ABC≌△ABF;
(2)当∠CAB=60°时,四边形ADFE为菱形,
证明:∵∠CAB=60°,
∴∠FAB=∠CAB=∠CAB=60°,
∴EF=AD=AE,
∴四边形ADFE是菱形,
故答案为60.
(3)∵四边形AEFD是菱形,设边长为a,∠AEF=∠CAB=60°,
∴△AEF、△AFD都是等边三角形,
由题意:2×![]() a2=6
a2=6![]() ,
,
∴a2=12,
∵a>0,
∴a=2![]() ,
,
∴AC=AE=2![]() ,
,
在RT△ACB中,∠ACB=90°,AC=2![]() ,∠CAB=60°,
,∠CAB=60°,
∴∠ABC=30°,
∴AB=2AC=4![]() ,BC=
,BC=![]() =6.
=6.
故答案为6.


科目:初中数学 来源: 题型:
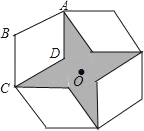
【题目】为了庆祝“六一儿童节”,六年级同学在班会课进行了趣味活动.小舟同学在模板上画出一个菱形ABCD,将它以点O为中心按顺时针方向分别旋转90°,180°,270°后得到如图所示的图形,其中∠ABC=120°,AB=2cm,然后小舟将此图形制作成一个靶子,那么当我们投飞镖时命中阴影部分的概率为( )
A. ![]() B. 2﹣
B. 2﹣![]() C.
C. ![]() -1D.
-1D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
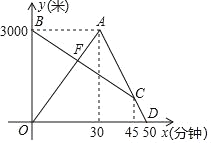
【题目】某个周末,小丽从家去园博园参观,同时妈妈参观结束从园博园回家,小丽刚到园博园就发现要下雨,于是立即按原路返回,追上妈妈后,两人一同回家(小丽和妈妈始终在同一条笔直的公路上行走)如图是两人离家的距离y(米)与小丽出发的时间x(分)之间的函数图象,请根据图象信息回答下列问题:
(1)求线段BC的解析式;
(2)求点F的坐标,并说明其实际意义;
(3)与按原速度回家相比,妈妈提前了几分钟到家?并直接写出小丽与妈妈何时相距800米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某手机店销售一部A型手机比销售一部B型手机获得的利润多50元,销售相同数量的A型手机和B型手机获得的利润分别为3000元和2000元.
(1)求每部A型手机和B型手机的销售利润分别为多少元?
(2)该商店计划一次购进两种型号的手机共110部,其中A型手机的进货量不超过B型手机的2倍.设购进B型手机n部,这110部手机的销售总利润为y元.
①求y关于n的函数关系式;
②该手机店购进A型、B型手机各多少部,才能使销售总利润最大?
(3)实际进货时,厂家对B型手机出厂价下调m(30<m<100)元,且限定商店最多购进B型手机80台.若商店保持两种手机的售价不变,请你根据以上信息及(2)中的条件,设计出使这110部手机销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:
我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
理解:
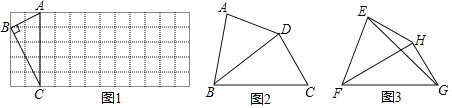
(1)如图1,已知Rt△ABC在正方形网格中,请你只用无刻度的直尺在网格中找到一点D,使四边形ABCD是以AC为“相似对角线”的四边形(保留画图痕迹,找出3个即可);
(2)如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC.
求证:BD是四边形ABCD的“相似对角线”;
(3)如图3,已知FH是四边形EFCH的“相似对角线”,∠EFH=∠HFG=30°,连接EG,若△EFG的面积为2![]() ,求FH的长.
,求FH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某图书馆计划选购甲、乙两种图书.已知甲种图书每本价格是乙种图书每本价格的2.5倍,用800元单独购买甲种图书比用800元单独购买乙种图书要少24本.求:
(1)乙种图书每本价格为多少元?
(2)如果该图书馆计划购买乙种图书的本数比购买甲种图书本数的2倍多8本,且用于购买甲、乙两种图书的总经费不超过1060元,那么该图书馆最多可以购买多少本甲种图书?
查看答案和解析>>
科目:初中数学 来源: 题型:
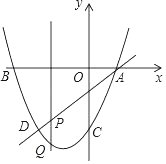
【题目】如图,抛物线y=x2+bx﹣3过点A(1,0),直线AD交抛物线于点D,点D的横坐标为﹣2,点P是线段AD上的动点.
(1)b= ,抛物线的顶点坐标为 ;
(2)求直线AD的解析式;
(3)过点P的直线垂直于x轴,交抛物线于点Q,连接AQ,DQ,当△ADQ的面积等于△ABD的面积的一半时,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016山西省)我省某苹果基地销售优质苹果,该基地对需要送货且购买量在2000kg﹣5000kg(含2000kg和5000kg)的客户有两种销售方案(客户只能选择其中一种方案):
方案A:每千克5.8元,由基地免费送货.
方案B:每千克5元,客户需支付运费2000元.
(1)请分别写出按方案A,方案B购买这种苹果的应付款y(元)与购买量x(kg)之间的函数表达式;
(2)求购买量x在什么范围时,选用方案A比方案B付款少;
(3)某水果批发商计划用20000元,选用这两种方案中的一种,购买尽可能多的这种苹果,请直接写出他应选择哪种方案.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() (
(![]() )与
)与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 左侧),与
左侧),与![]() 轴交于点
轴交于点![]() ,该抛物线的顶点
,该抛物线的顶点![]() 的纵坐标是
的纵坐标是![]() .
.

(1)求点![]() 、
、![]() 的坐标;
的坐标;
(2)设直线与直线![]() 关于该抛物线的对称轴对称,求直线的表达式;
关于该抛物线的对称轴对称,求直线的表达式;
(3)平行于![]() 轴的直线
轴的直线![]() 与抛物线交于点
与抛物线交于点![]() 、
、![]() ,与直线交于点
,与直线交于点![]() .若
.若![]() ,结合函数图象,求
,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com