
【题目】定义:
我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
理解:
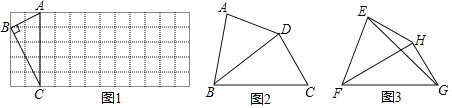
(1)如图1,已知Rt△ABC在正方形网格中,请你只用无刻度的直尺在网格中找到一点D,使四边形ABCD是以AC为“相似对角线”的四边形(保留画图痕迹,找出3个即可);
(2)如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC.
求证:BD是四边形ABCD的“相似对角线”;
(3)如图3,已知FH是四边形EFCH的“相似对角线”,∠EFH=∠HFG=30°,连接EG,若△EFG的面积为2![]() ,求FH的长.
,求FH的长.
【答案】(1)见解析;(2)证明见解析;(3)FH=2![]() .
.
【解析】(1)先求出AB,BC,AC,再分情况求出CD或AD,即可画出图形;
(2)先判断出∠A+∠ADB=140°=∠ADC,即可得出结论;
(3)先判断出△FEH∽△FHG,得出FH2=FEFG,再判断出EQ=![]() FE,继而求出FGFE=8,即可得出结论.
FE,继而求出FGFE=8,即可得出结论.
(1)由图1知,AB=![]() ,BC=2
,BC=2![]() ,∠ABC=90°,AC=5,
,∠ABC=90°,AC=5,
∵四边形ABCD是以AC为“相似对角线”的四边形,
当∠ACD=90°时,△ACD∽△ABC或△ACD∽△CBA,
∴![]() 或
或![]() ,
,
∴CD=10或CD=2.5
同理:当∠CAD=90°时,AD=2.5或AD=10,
(2)∵∠ABC=80°,BD平分∠ABC,
∴∠ABD=∠DBC=40°,
∴∠A+∠ADB=140°
∵∠ADC=140°,
∴∠BDC+∠ADB=140°,
∴∠A=∠BDC,
∴△ABD∽△BDC,
∴BD是四边形ABCD的“相似对角线”;
(3)如图3,
∵FH是四边形EFGH的“相似对角线”,
∴△EFH与△HFG相似,
∵∠EFH=∠HFG,
∴△FEH∽△FHG,
∴![]() ,
,
∴FH2=FEFG,
过点E作EQ⊥FG于Q,
∴EQ=FEsin60°=![]() FE,
FE,
∵![]() FG×EQ=2
FG×EQ=2![]() ,
,
∴![]() FG×
FG×![]() FE=2
FE=2![]() ,
,
∴FGFE=8,
∴FH2=FEFG=8,
∴FH=2![]() .
.


科目:初中数学 来源: 题型:
【题目】解不等式组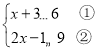 .请结合题意填空,完成本题的解答
.请结合题意填空,完成本题的解答
(Ⅰ)解不等式①,得__________;
(Ⅱ)解不等式②,得__________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:

(Ⅳ)原不等式组的解集为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
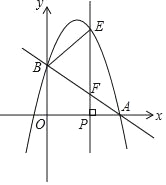
【题目】如图,在平面直角坐标系中,直线y=-![]() x+2分别交x轴、y轴于点A、B,抛物线y=﹣x2+bx+c经过点A、B.点P是x轴上一个动点,过点P作垂直于x轴的直线分别交抛物线和直线AB于点E和点F.设点P的横坐标为m.
x+2分别交x轴、y轴于点A、B,抛物线y=﹣x2+bx+c经过点A、B.点P是x轴上一个动点,过点P作垂直于x轴的直线分别交抛物线和直线AB于点E和点F.设点P的横坐标为m.
(1)点A的坐标为 .
(2)求这条抛物线所对应的函数表达式.
(3)点P在线段OA上时,若以B、E、F为顶点的三角形与△FPA相似,求m的值.
(4)若E、F、P三个点中恰有一点是其它两点所连线段的中点(三点重合除外),称E、F、P三点为“共谐点”.直接写出E、F、P三点成为“共谐点”时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于![]() 的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )
的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )

A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,Rt△OCD的一边OC在x轴上,∠OCD=90°,点D在第一象限,OC=6,DC=4,反比例函数的图象经过OD的中点A.
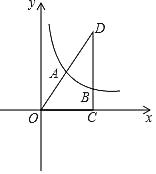
(1)求该反比例函数的解析式;
(2)若该反比例函数的图象与Rt△OCD的另一边DC交于点B,求过A、B两点的直线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A,交AB于点D,交CA的延长线于点E,过点E作AB的平行线交⊙A于点F,连接AF,BF,DF.
(1)求证:△ABC≌△ABF;
(2)填空:
①当∠CAB= °时,四边形ADFE为菱形;
②在①的条件下,BC= cm时,四边形ADFE的面积是6![]() cm2.
cm2.

查看答案和解析>>
科目:初中数学 来源: 题型:
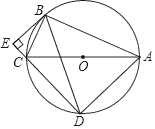
【题目】如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,BD=BA,BE⊥DC交DC的延长线于点E.
(1)若∠BAD=70°,则∠BCA= °;
(2)若AB=12,BC=5,求DE的长:
(3)求证:BE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的
为直径的![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 是
是![]() 的延长线上一点,且∠PDB=
的延长线上一点,且∠PDB=![]() ∠A,连接
∠A,连接![]() ,
,![]() .
.
(1)求证:![]() 是
是![]() 的切线.
的切线.
(2)填空:
①当![]() 的度数为______时,四边形
的度数为______时,四边形![]() 是菱形;
是菱形;
②当![]() 时,
时,![]() 的面积为_________.
的面积为_________.
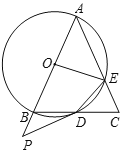
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】丁老师为了解所任教的两个班的学生数学学习情况,对数学进行了一次测试,获得了两个班的成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
①A、B两班学生(两个班的人数相同)数学成绩不完整的频数分布直方图如下(数据分成5组:x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100):
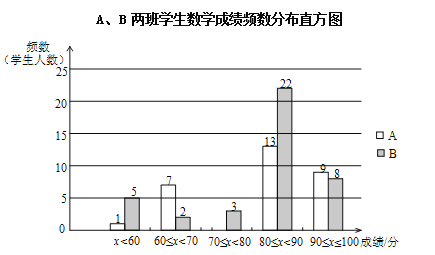
②A、B两班学生测试成绩在80≤x<90这一组的数据如下:
A班:80 80 82 83 85 85 86 87 87 87 88 89 89
B班:80 80 81 81 82 82 83 84 84 85 85 86 86 86 87 87 87 87 87 88 88 89
③A、B两班学生测试成绩的平均数、中位数、方差如下:
平均数 | 中位数 | 方差 | |
A班 | 80.6 | m | 96.9 |
B班 | 80.8 | n | 153.3 |
根据以上信息,回答下列问题:
(1)补全数学成绩频数分布直方图;
(2)写出表中m、n的值;
(3)请你对比分析A、B两班学生的数学学习情况(至少从两个不同的角度分析).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com